题目内容
【题目】已知sinα+cosα= ![]() ,α∈(0,
,α∈(0, ![]() ),sin(β﹣
),sin(β﹣ ![]() )=
)= ![]() ,β∈(
,β∈( ![]() ,
, ![]() ).
).
(1)求sin2α和tan2α的值;
(2)求cos(α+2β)的值.
【答案】
(1)解:由题意得(sinα+cosα)2= ![]() ,
,
即1+sin2α= ![]() ,∴sin2α=
,∴sin2α= ![]() .
.
又2α∈(0, ![]() ),∴cos2α=
),∴cos2α= ![]() =
= ![]() ,∴tan2α=
,∴tan2α= ![]() =
= ![]()
(2)解:∵β∈( ![]() ,
, ![]() ),β﹣
),β﹣ ![]() ∈(0,
∈(0, ![]() ),∴cos(β﹣
),∴cos(β﹣ ![]() )=
)= ![]() ,
,
于是sin2(β﹣ ![]() )=2sin(β﹣
)=2sin(β﹣ ![]() )cos(β﹣
)cos(β﹣ ![]() )=
)= ![]() .
.
又sin2(β﹣ ![]() )=﹣cos2β,∴cos2β=﹣
)=﹣cos2β,∴cos2β=﹣ ![]() .
.
又2β∈( ![]() ,π),∴sin2β=
,π),∴sin2β= ![]() .
.
又cos2α= ![]() =
= ![]() ,
,
∴cosα= ![]() ,sinα=
,sinα= ![]() (α∈(0,
(α∈(0, ![]() )).
)).
∴cos(α+2β)=cosαcos2β﹣sinαsin2β
= ![]() ×(﹣
×(﹣ ![]() )﹣
)﹣ ![]() ×
× ![]() =﹣
=﹣ ![]()
【解析】(1)把已知条件两边平方,然后利用同角三角函数间的关系及二倍角的正弦函数公式化简可得sin2α的值,根据2α的范围利用同角三角函数间的关系求出cos2α即可得到tan2α的值;(2)根据β的范围求出 ![]() 的范围,由sin(
的范围,由sin( ![]() )的值利用同角三角函数间的关系求出cos(
)的值利用同角三角函数间的关系求出cos( ![]() )的值,然后利用二倍角的正弦函数公式及同角三角函数间的关系分别求出sin2β和cos2β的值,根据第一问分别求出sinα和cosα的值,把所求的式子利用两角和的余弦函数公式化简后,将每个三角函数值代入即可求出.
)的值,然后利用二倍角的正弦函数公式及同角三角函数间的关系分别求出sin2β和cos2β的值,根据第一问分别求出sinα和cosα的值,把所求的式子利用两角和的余弦函数公式化简后,将每个三角函数值代入即可求出.
【考点精析】本题主要考查了两角和与差的余弦公式和二倍角的正弦公式的相关知识点,需要掌握两角和与差的余弦公式:![]() ;二倍角的正弦公式:
;二倍角的正弦公式:![]() 才能正确解答此题.
才能正确解答此题.

【题目】选修4-4:坐标系与参数方程
已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数, ![]() ).
).
(Ⅰ)把曲线![]() 的极坐标方程化为直角坐标方程,并说明曲线
的极坐标方程化为直角坐标方程,并说明曲线![]() 的形状;
的形状;
(Ⅱ)若直线![]() 经过点
经过点![]() ,求直线
,求直线![]() 被曲线
被曲线![]() 截得的线段
截得的线段![]() 的长.
的长.
【题目】如图,F1,F2分别是椭圆C:![]() 的左、右焦点,A是椭圆C的顶点,B是直线AF2与椭圆C的另一个交点,∠F1AF2=60°.
的左、右焦点,A是椭圆C的顶点,B是直线AF2与椭圆C的另一个交点,∠F1AF2=60°.
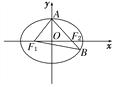
(1)求椭圆C的离心率;
(2)已知△AF1B的面积为40![]() ,求a,b的值.
,求a,b的值.
【题目】从甲、乙两名学生中选拔一人参加射箭比赛,为此需要对他们的射箭水平进行测试.现这两名学生在相同条件下各射箭10次,命中的环数如表:
甲 | 8 | 9 | 7 | 9 | 7 | 6 | 10 | 10 | 8 | 6 |
乙 | 10 | 9 | 8 | 6 | 8 | 7 | 9 | 7 | 8 | 8 |
(1)计算甲、乙两人射箭命中环数的平均数和标准差;
(2)比较两个人的成绩,然后决定选择哪名学生参加射箭比赛.