题目内容
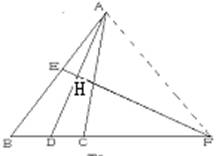
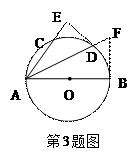
已知:如图,△ABC中,AD平分∠BAC,AD的垂直平分线交AB于点E,交AD于点H,交AC于点G,交BC的延长线于点F,求证:DF2=CF•BF.

同解析
证明:连AF, ∵FH垂直平分AD,
∴FA=FD, ∠FAD=∠FDA,
∵AD平分∠BAC,∴∠CAD=∠BAD,
∴∠FAD-∠CAD=∠FDA-∠BAD,
∵∠B=∠FDA-∠BAD,
∴∠FAC=∠B,又∠AFC公共,
∴△AFC∽△BFA,∴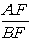 =
=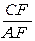 ,
,
∴AF2=CF•BF,∴DF2=CF•BF.
∴FA=FD, ∠FAD=∠FDA,
∵AD平分∠BAC,∴∠CAD=∠BAD,
∴∠FAD-∠CAD=∠FDA-∠BAD,
∵∠B=∠FDA-∠BAD,
∴∠FAC=∠B,又∠AFC公共,
∴△AFC∽△BFA,∴
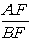 =
=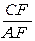 ,
,∴AF2=CF•BF,∴DF2=CF•BF.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 的角平分线
的角平分线 的延长线交它的外接圆于点
的延长线交它的外接圆于点 .
.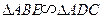 ;
;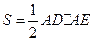 ,求
,求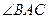 的大小.
的大小.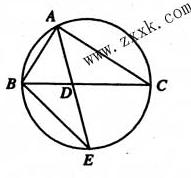
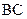 的中点,DE⊥AC交AC的延长线于点F.
的中点,DE⊥AC交AC的延长线于点F.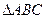 中,AB=AC,过点A的直线与其外接圆交于点P,交BC延长线于点D。
中,AB=AC,过点A的直线与其外接圆交于点P,交BC延长线于点D。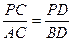 ;
;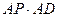 的值。
的值。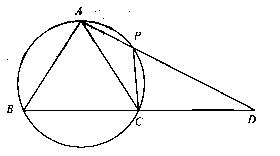
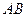 =6cm,
=6cm,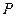 是
是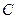 ,连接
,连接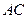 ,若
,若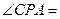 30°,PC
30°,PC  = cm.
= cm.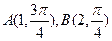 ,则|AB|=" " .
,则|AB|=" " .