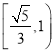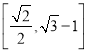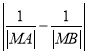题目内容
【题目】直线l：x﹣y
0将圆O：
分成的两部分的面积之比为（ ）
A.(4π
):(8π
)B.(4π﹣3
):(8π+3)
C.(2π﹣2):(10π+2)D.(2π﹣3):(10π+3)
【答案】B
【解析】
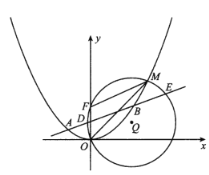
根据题意，设直线l与圆O：x2+y2=4交于点MN，过点O作OP⊥MN，垂足为点P，求出|OP|的值，结合直线与圆的位置关系可得∠MON
以及|MN|=2
；进而计算可得S△MON和S扇形OMN的值，据此可得直线l将圆O分成的两部分的面积，计算即可得答案.
解：根据题意，设直线l与圆O：x2+y2=4交于点MN，过点O作OP⊥MN，垂足为点P，
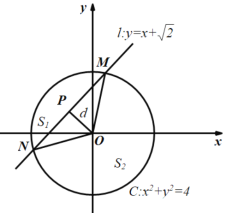
则点O到直线l的距离|OP|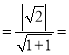
1，
又由圆O：x2+y2=4的半径|OM|=r=2，则∠MOP
，则∠MON；
同时|MP|
，则|MN|=2，
且S△MON
|OP|×|MN|
，
则S扇形OMN
r2
，
则劣弧对应的弓形的面积S1
，
另一部分的面积S2=πr2﹣S1=4π﹣(
)
，
故两部分的面积之比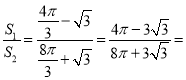
(4π﹣3)：(8π+3).
故选：B.
练习册系列答案
相关题目
