题目内容
【题目】已知函数g(x)=ex﹣ax2﹣ax,h(x)=ex﹣2x﹣lnx.其中e为自然对数的底数.
(1)若f(x)=h(x)﹣g(x).
①讨论f(x)的单调性;
②若函数f(x)有两个不同的零点,求实数a的取值范围.
(2)已知a>0,函数g(x)恰有两个不同的极值点x1,x2,证明:![]() .
.
【答案】(1)①见解析;②(0,1);(2)证明见解析
【解析】
(1)①对![]() 求导,分别讨论
求导,分别讨论![]() 与
与![]() 的情况即可;
的情况即可;
②由①若![]() 有两个不同的零点,则
有两个不同的零点,则![]() ,由于当x→0时,f(x)→+∞;当x→+∞时,f(x)→+∞,则只需使得
,由于当x→0时,f(x)→+∞;当x→+∞时,f(x)→+∞,则只需使得![]() 即可,进而求解;
即可,进而求解;
(2)先对![]() 求导,由题可得
求导,由题可得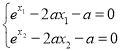 ,两式相减可得
,两式相减可得![]() ,转化
,转化![]() 为
为![]() ,设
,设![]() ,即证
,即证![]() ,进而利用导函数判断单调性证明即可.
,进而利用导函数判断单调性证明即可.
(1)f(x)=h(x)﹣g(x)=ex﹣2x﹣lnx﹣ex+ax2+ax=ax2+(a﹣2)x﹣lnx(x>0),
①![]() (x>0),
(x>0),
(i)当a≤0时,f′(x)<0,函数f(x)在(0,+∞)上递减;
(ii)当a>0时,令f′(x)>0,解得![]() ;令f′(x)<0,解得
;令f′(x)<0,解得![]() ,
,
∴函数f(x)在![]() 递减,在
递减,在![]() 递增;
递增;
综上,当a≤0时,函数f(x)在(0,+∞)上单调递减;
当a>0时,函数f(x)在![]() 上单调递减,在
上单调递减,在![]() 上单调递增
上单调递增
②由①知,若a≤0,函数f(x)在(0,+∞)上单调递减,不可能有两个不同的零点,故a>0;
且当x→0时,f(x)→+∞;当x→+∞时,f(x)→+∞;
故要使函数f(x)有两个不同的零点,只需![]() ,即
,即![]() ,
,
又函数![]() 在(0,+∞)上为增函数,且
在(0,+∞)上为增函数,且![]() ,故
,故![]() 的解集为(0,1),
的解集为(0,1),
故实数a的取值范围为(0,1)
(2)证明: g′(x)=ex﹣2ax﹣a,依题意,则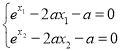 ,两式相减得,
,两式相减得,![]() ,
,
因为a>0,要证![]() ,即证
,即证![]() ,即证
,即证![]() ,
,
两边同除以![]() ,即证
,即证![]() ,
,
令t=x1﹣x2(t<0),即证![]() ,
,
令![]() ,则
,则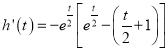 ,
,
令![]() ,则
,则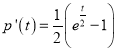 ,
,
当t<0时,p′(t)<0,所以p(t)在(﹣∞,0)上递减,
∴p(t)>p(0)=0,
∴h′(t)<0,
∴h(t)在(﹣∞,0)上递减,
∴h(t)>h(0)=0,即![]() ,
,
故![]() .
.

 阅读快车系列答案
阅读快车系列答案