��Ŀ����
����Ŀ�����壺������{an}�г�ȡm��m��N��m��3�������{an}�еĴ��������γ�һ��������{bn}�����{bn}Ϊ{an}�������У���{bn}�ɵȲ��ȱȣ������{bn}Ϊ{an}�ĵȲ��ȱȣ������У�
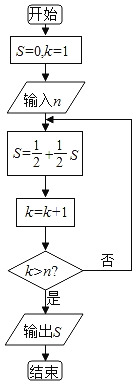
��1��������{an}��ǰn���ΪSn����֪![]() ��
��
��������{an}��ͨ�ʽ��
������{an}�Ƿ���ڵȲ������У������ڣ�����Ȳ������У��������ڣ���˵�����ɣ�
��2����֪����{an}��ͨ�ʽΪan��n+a��a��Q+����֤����{an}���ڵȱ������У�
���𰸡���1����![]() ���ڲ����ڵȲ������У���������2��������
���ڲ����ڵȲ������У���������2��������
��������
��1���ٸ���![]() ����n��1ʱ��
����n��1ʱ��![]() ����n��2ʱ���õ�
����n��2ʱ���õ�![]() ����ʽ�������.�ڼ��������{an}�г�3��ak��al��am��k��l��m���ɵȲ���õȲ�������2al��ak+am����2��2l��1��2k��1+2m��1��
����ʽ�������.�ڼ��������{an}�г�3��ak��al��am��k��l��m���ɵȲ���õȲ�������2al��ak+am����2��2l��1��2k��1+2m��1��
����ã�2��2l��k��1+2m��k����������ż���ж�.���������{an}�г�m��m��N��m��4�����ǰ����سɵȲ����У���������֤.
��2����������{an}�д���3��n0+a��n0+a+k��n0+a+l��k��l���ɵȱȣ���n0+a��b����b��Q+���ʿ���![]() ��p��q�ǻ��ʵ��������������ݵȱ������
��p��q�ǻ��ʵ��������������ݵȱ������![]() ����
����![]() ��ȡk��q����l��2k+pq������֤��b+k��2=b��b+l���Ƿ��������.
��ȡk��q����l��2k+pq������֤��b+k��2=b��b+l���Ƿ��������.
��1������Ϊ![]() �����Ե�n��1ʱ��
�����Ե�n��1ʱ��![]() ��
��
��n��2ʱ��![]() ������
������![]() ��
��
���Ͽ�֪��![]() ��
��
�ڼ��������{an}�г�3��ak��al��am��k��l��m���ɵȲ
��2al��ak+am����2��2l��1��2k��1+2m��1��
����ã�2��2l��k��1+2m��k��
��Ϊk��l��m������l��k��0��m��k��0����l��k��m��k����������
����2��2l��kΪż����1+2m��kΪ����������2��2l��k��1+2m��k��������
��ˣ�����{an}����������Ȳ������У�
��������{an}�г�m��m��N��m��4�����ǰ����سɵȲ����У���������
���Ͽ�֪������{an}�����ڵȲ������У�
��2����������{an}�д���3��n0+a��n0+a+k��n0+a+l��k��l���ɵȱȣ�
��n0+a��b����b��Q+���ʿ���![]() ��p��q�ǻ��ʵ�����������
��p��q�ǻ��ʵ�����������
��������![]() ��
��
�������㣨b+k��2��b��b+l������������![]() ��
��
ȡk��q����l��2k+pq��
��ʱ![]() ��
��![]() ��
��
�ʴ�ʱ��b+k��2��b��b+l��������
�������{an}�д���3��n0+a��n0+a+k��n0+a+l��k��l���ɵȱȣ�
��������{an}���ڵȱ������У�