题目内容
过抛物线y2=4x的焦点F且斜率为k(k>0)的直线交抛物线于A、B两点,若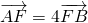 ,则斜率k的值为
,则斜率k的值为
- A.1
- B.2
- C.

- D.

D
分析:先设点A,B的坐标,求出直线方程后与抛物线方程联立消去y得到关于x的一元二次方程,求出两根,再根据向量的有关知识得到坐标的关系,进而代入抛物线的方程中得到答案
解答:∵抛物线 C:y2=4x焦点F(1,0),准线x=-1,则直线AB的方程为y=k(x-1)
联立方程 可得k2x2-2(2+k2)x+k2=0
可得k2x2-2(2+k2)x+k2=0
设A(x1,y1),B(x2,y2),则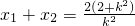 ,y1+y2=k(x1+x2-2)=
,y1+y2=k(x1+x2-2)=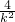 •k=
•k=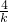 ①
①
∴ ,
,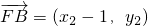
∵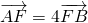 ,
,
∴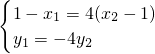 即
即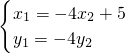 ②
②
①②联立可得,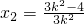 ,
,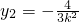
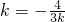 ,代入抛物线方程y2=4x可得
,代入抛物线方程y2=4x可得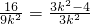 ×4
×4
∴9k2=16
∵k>0
∴k=
故选D
点评:本题主要考查直线与抛物线的位置关系,方程的根与系数关系的应用,抛物线定义的应用以及向量的坐标表示的应用
分析:先设点A,B的坐标,求出直线方程后与抛物线方程联立消去y得到关于x的一元二次方程,求出两根,再根据向量的有关知识得到坐标的关系,进而代入抛物线的方程中得到答案
解答:∵抛物线 C:y2=4x焦点F(1,0),准线x=-1,则直线AB的方程为y=k(x-1)
联立方程
 可得k2x2-2(2+k2)x+k2=0
可得k2x2-2(2+k2)x+k2=0设A(x1,y1),B(x2,y2),则
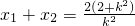 ,y1+y2=k(x1+x2-2)=
,y1+y2=k(x1+x2-2)=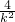 •k=
•k=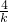 ①
①∴
 ,
,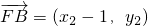
∵
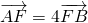 ,
,∴
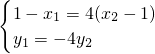 即
即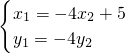 ②
②①②联立可得,
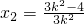 ,
,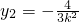
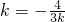 ,代入抛物线方程y2=4x可得
,代入抛物线方程y2=4x可得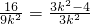 ×4
×4∴9k2=16
∵k>0
∴k=

故选D
点评:本题主要考查直线与抛物线的位置关系,方程的根与系数关系的应用,抛物线定义的应用以及向量的坐标表示的应用

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
倾斜角为
的直线过抛物线y2=4x的焦点且与抛物线交于A,B两点,则|AB|=( )
| π |
| 4 |
A、
| ||
B、8
| ||
| C、16 | ||
| D、8 |
过抛物线y2=4x的焦点F的直线交抛物线于A、B两点,点O是坐标原点,若|AF|=5,则△AOB的面积为( )
| A、5 | ||
B、
| ||
C、
| ||
D、
|