题目内容
已知函数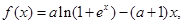 (其中
(其中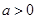 ) ,点
) ,点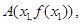
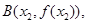
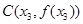 从左到右依次是函数
从左到右依次是函数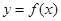 图象上三点,且
图象上三点,且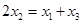 .
.
(1)证明: 函数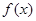 在
在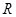 上是减函数;
上是减函数;
(2)求证:⊿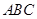 是钝角三角形;
是钝角三角形;
(3)试问,⊿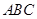 能否是等腰三角形?若能,求⊿
能否是等腰三角形?若能,求⊿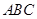 面积的最大值;若不能,请说明理由.
面积的最大值;若不能,请说明理由.
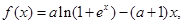 (其中
(其中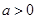 ) ,点
) ,点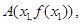
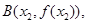
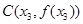 从左到右依次是函数
从左到右依次是函数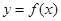 图象上三点,且
图象上三点,且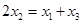 .
.(1)证明: 函数
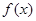 在
在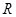 上是减函数;
上是减函数;(2)求证:⊿
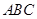 是钝角三角形;
是钝角三角形;(3)试问,⊿
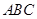 能否是等腰三角形?若能,求⊿
能否是等腰三角形?若能,求⊿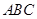 面积的最大值;若不能,请说明理由.
面积的最大值;若不能,请说明理由.(1)见解析(2) 见解析(3) ⊿ 不可能为等腰三角形
不可能为等腰三角形
 不可能为等腰三角形
不可能为等腰三角形【错解分析】函数历来是高中数学最重要的内容,不仅适合单独命题,而且可以综合运用于其它内容.函数是中学数学的最重要内容,它既是工具,又是方法和思想
【正解】
(Ⅰ)
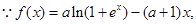
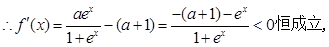
所以函数
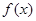 在
在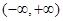 上是单调减函数.
上是单调减函数.
(Ⅱ) 证明:据题意
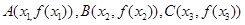 且x1<x2<x3,
且x1<x2<x3,由(Ⅰ)知f (x1)>f (x2)>f (x3), x2=
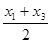
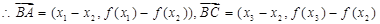
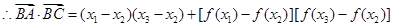
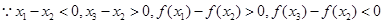
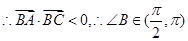 即⊿
即⊿ 是钝角三角形
是钝角三角形(Ⅲ)假设⊿
 为等腰三角形,则只能是
为等腰三角形,则只能是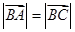
即
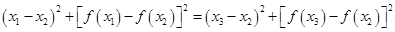
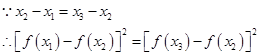
即
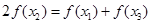
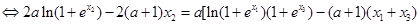
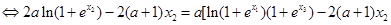
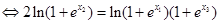
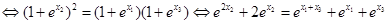
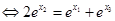 ①而事实上,
①而事实上, 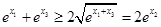 ②
②由于
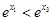 ,故(2)式等号不成立.这与
,故(2)式等号不成立.这与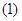 式矛盾. 所以⊿
式矛盾. 所以⊿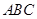 不可能为等腰三角形
不可能为等腰三角形【点评】函数的综合问题,这类问题涉及的知识点多,与数列、不等式等知识加以综合。主要考察函数的奇偶性、单调性、极值、导数、不等式等基础知识,考查运用导数研究函数性质的方法,以及分类与整合、转化与化归等数学思想方法,考查分析问题和解决问题的能力.

练习册系列答案
相关题目
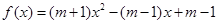
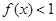 的解集为
的解集为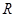 ,求
,求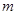 的取值范围;
的取值范围;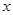 的不等式
的不等式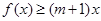 ;
;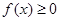 对一切
对一切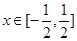 恒成立,求
恒成立,求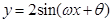 为偶函数(0<θ<π), 其图象与直线y=2的交点的横坐标为
为偶函数(0<θ<π), 其图象与直线y=2的交点的横坐标为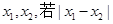 的最小值为π,则( )
的最小值为π,则( )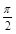
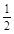 ,θ=
,θ=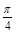
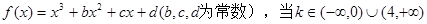 时,
时,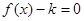 只有一个实根;当
只有一个实根;当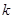 ∈(0,4)时,
∈(0,4)时,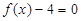 和
和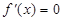 有一个相同的实根;
有一个相同的实根;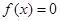 和
和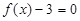 的任一实根大于
的任一实根大于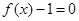 的任一实根;
的任一实根; 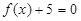 的任一实根小于
的任一实根小于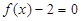 的任一实根.
的任一实根.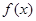 满足:x≥4,则
满足:x≥4,则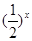 ;当x<4时
;当x<4时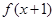 ,则
,则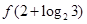 =
=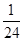
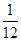
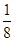
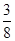
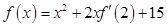 ,在闭区间
,在闭区间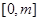 上有最大值15,最小值-1,则
上有最大值15,最小值-1,则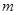 的取值范围是( )
的取值范围是( )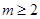
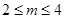
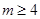

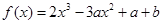 (其中a,b为实常数)。
(其中a,b为实常数)。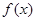 的单调区间:
的单调区间: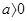 时,函数
时,函数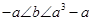 :
: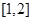 上是减函数,设关于x的方程
上是减函数,设关于x的方程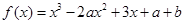 的两个非零实数根为
的两个非零实数根为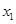 ,
,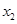 。试问是否存在实数m,使得
。试问是否存在实数m,使得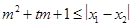 对任意满足条件的a及t
对任意满足条件的a及t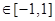 恒成立?若存在,求m的取值范围;若不存在,请说明理由。
恒成立?若存在,求m的取值范围;若不存在,请说明理由。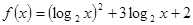 ,
,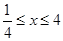 ,
,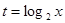 ,求
,求 取值范围;
取值范围; 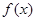 的最值,并给出函数取最值时对应的x的值。
的最值,并给出函数取最值时对应的x的值。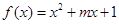 的图像关于直线
的图像关于直线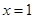 对称的充要条件是 ;
对称的充要条件是 ;