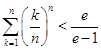题目内容
已知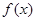 为定义在
为定义在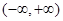 上的可导函数,且
上的可导函数,且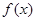
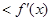 对于任意
对于任意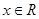 恒成立,则( )
恒成立,则( )
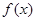 为定义在
为定义在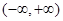 上的可导函数,且
上的可导函数,且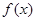
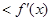 对于任意
对于任意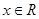 恒成立,则( )
恒成立,则( )A. , ,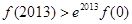 |
B.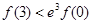 , ,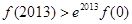 |
C. , ,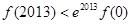 |
D.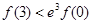 , ,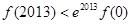 |
A
试题分析:因为
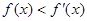 ,从而
,从而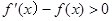 ,从而
,从而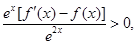
从而
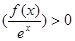 ,从而函数
,从而函数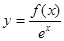 单调递增,故
单调递增,故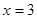 时,函数值大于
时,函数值大于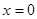 时的函数值,
时的函数值,从而
 ,同理
,同理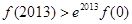 .
.点评:本题主要考查函数的单调性与其导函数的正负情况之间的关系,即导函数大于0时原函数单调递增,当导函数小于0时原函数单调递减.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 为定义在
为定义在 上的奇函数,当
上的奇函数,当 时,
时,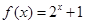 ,则当
,则当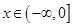 时,
时,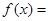 _______________.
_______________.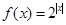 ,则下列结论中正确的是( )
,则下列结论中正确的是( )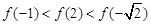
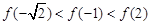
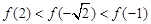
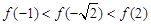
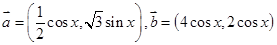 函数
函数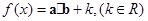
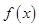 的单调增区间;
的单调增区间;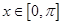 时,
时,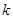 的值.
的值.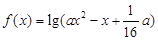 的定义域为R;命题q:不等式
的定义域为R;命题q:不等式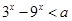 对任意
对任意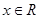 恒成立.
恒成立. 的取值范围;
的取值范围;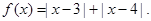
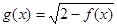 的定义域;
的定义域;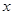 满足
满足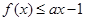 ,试求实数
,试求实数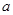 的取值范围.
的取值范围.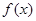 的定义域为A,若
的定义域为A,若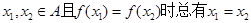 则称
则称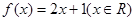 是单函数.下列命题:
是单函数.下列命题: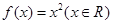 是单函数;
是单函数;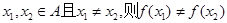 ;
;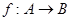 为单函数,则对于任意b
为单函数,则对于任意b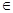 B,它至多有一个原象;
B,它至多有一个原象;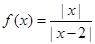 是偶函数;
是偶函数;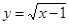 的值域为
的值域为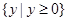 ;
;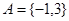 ,
,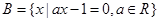 ,若
,若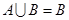 ,则
,则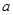 的取值集合为
的取值集合为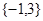 ;
;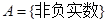 ,
,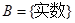 ,对应法则
,对应法则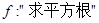 ,则
,则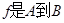 的映射;
的映射;
 x;
x;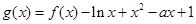 存在两个零点,求a的取值范围
存在两个零点,求a的取值范围