题目内容
设命题p:函数
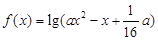 的定义域为R;命题q:不等式
的定义域为R;命题q:不等式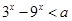 对任意
对任意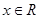 恒成立.
恒成立.(Ⅰ)如果p是真命题,求实数
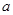 的取值范围;
的取值范围;(Ⅱ)如果命题“p或q”为真命题且“p且q”为假命题,求实数
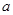 的取值范围.
的取值范围.(Ⅰ)实数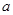 的取值范围是
的取值范围是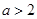 .(Ⅱ)实数
.(Ⅱ)实数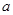 的取值范围是
的取值范围是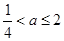 .
.
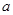 的取值范围是
的取值范围是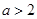 .(Ⅱ)实数
.(Ⅱ)实数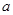 的取值范围是
的取值范围是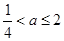 .
.试题分析:(Ⅰ)由题意:
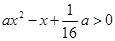 对任意
对任意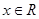 恒成立,
恒成立,当
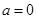 时,不符题意,舍去,
时,不符题意,舍去,当
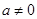 时,
时,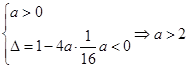 ,
,所以实数
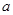 的取值范围是
的取值范围是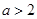 .
.(Ⅱ)设
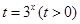 ,
,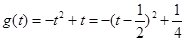 ,
,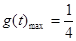 ,当
,当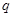 为真命题时,有
为真命题时,有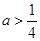 ,
,∵命题“p或q”为真命题且“p且q”为假命题,∴
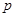 与
与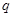 一个为真,一个为假,
一个为真,一个为假,当
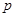 真
真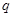 假,则
假,则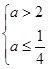 ,无解,
,无解,当
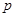 假
假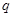 真,则
真,则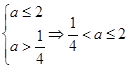 ,
,综上,实数
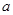 的取值范围是
的取值范围是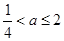 .
.点评:中档题,涉及复合命题,综合性较强。注意对于“p或q”p,q有一个真命题,其即为真命题,“p且q”中,p,q有一假命题,其即为假命题。

练习册系列答案
相关题目
 ,
,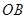 是某地一个湖泊的两条互相垂直的湖堤,线段
是某地一个湖泊的两条互相垂直的湖堤,线段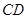 和曲线段
和曲线段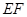 分别是湖泊中的一座栈桥和一条防波堤.为观光旅游的需要,拟过栈桥
分别是湖泊中的一座栈桥和一条防波堤.为观光旅游的需要,拟过栈桥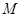 分别修建与
分别修建与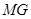 、
、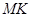 ,且以
,且以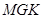 .建立如图2所示的直角坐标系,测得线段
.建立如图2所示的直角坐标系,测得线段 ,曲线段
,曲线段 ,设点
,设点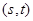 ,记
,记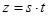 .(题中所涉及的长度单位均为米,栈桥和防波堤都不计宽度)
.(题中所涉及的长度单位均为米,栈桥和防波堤都不计宽度)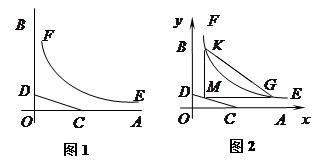
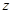 的取值范围;
的取值范围; 关于
关于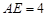 米,
米,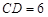 米. 为了合理利用这块钢板,将在五边形
米. 为了合理利用这块钢板,将在五边形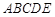 内截取一个矩形块
内截取一个矩形块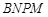 ,使点
,使点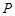 在边
在边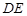 上. 则矩形
上. 则矩形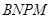 面积的最大值为____ 平方米 .
面积的最大值为____ 平方米 . 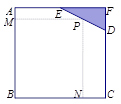
 与当天的空气水平可见度
与当天的空气水平可见度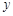 (千米)的情况,表2是某气象观测点记录的北京1月1日到1月30日AQI指数频数统计结果,
(千米)的情况,表2是某气象观测点记录的北京1月1日到1月30日AQI指数频数统计结果, 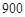
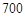
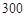

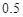
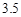

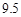
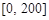
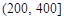
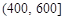
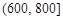

 ,根据表1的数据,求出
,根据表1的数据,求出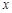 的线性回归方程;
的线性回归方程; ,
,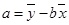 )
)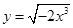 相同的是( )
相同的是( )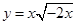
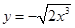
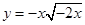
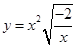
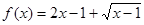 的值域为__________.
的值域为__________.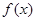 为定义在
为定义在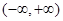 上的可导函数,且
上的可导函数,且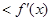 对于任意
对于任意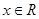 恒成立,则( )
恒成立,则( ) ,
,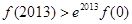
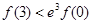 ,
,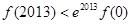
 、纵边
、纵边 设计为多少米时,才能使围成的网箱中筛网的总长度最小?
设计为多少米时,才能使围成的网箱中筛网的总长度最小?
 满足
满足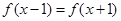 ,当
,当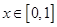 时,
时, 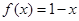 ,则关于
,则关于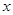 的方程
的方程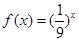 在
在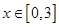 上解的个数是( )
上解的个数是( )