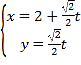题目内容
【题目】(1)若正整数n可以表示成![]() )的形式,则称n为“好数”.试求与2的正整数次幂相邻的所有好数.(2) 试求不定方程
)的形式,则称n为“好数”.试求与2的正整数次幂相邻的所有好数.(2) 试求不定方程![]() 的所有非负整数解
的所有非负整数解![]()
【答案】(1)9;(2)(1,0,0),(1,1,0),(2,1,0),(3,2,0),(4,l,1),(2,0,1).
【解析】
(1)设所求的好数为n,![]()
于是,存在正整数t (t>1),使得![]() 显然,
显然,![]() 为奇数.
为奇数.
若b为奇数,则![]() ①
①
而![]() 是奇数个奇数相加减的结果仍然是奇数,只可能是l,代入
是奇数个奇数相加减的结果仍然是奇数,只可能是l,代入
式①得b=l,这与b≥2矛盾.
若b为偶数,则![]()
若![]() ,则
,则![]()
所以,t=1.矛盾
若![]() ,
,
但![]() ,
,
故![]()
综上,所求的所有好数只有一个n=9.
(2)显然,![]() ≥1.当z=0时,若y≤1,易得方程的三组解(1,0,0),(1,1,0),(2,l,0);
≥1.当z=0时,若y≤1,易得方程的三组解(1,0,0),(1,1,0),(2,l,0);
若y≥2,由(1)的结论易知此时方程只有一组解(3,2,0).
当z≥l时,显然,![]() .
.
易知当且仅当![]() (mod 4)时,
(mod 4)时,![]() ;
;
当且仅当![]() (mod 4)时,
(mod 4)时,![]()
若![]() ②
②
则![]() ,此时,
,此时,![]()
设![]() 对式②两边模4得
对式②两边模4得![]()
于是,y是奇数.设![]()
则式②变为![]() ,
,
即![]()
由![]() ,有
,有![]()
结合(1)的结论可知满足式③![]() 只有(1,0)一对,代人式④得z=1.
只有(1,0)一对,代人式④得z=1.
此时,原方程的一组解为(4,l,1).
若![]() , ⑤
, ⑤
则![]() ,此时,
,此时,![]()
设![]() 则
则![]() ⑥
⑥
当k=0时,y=0,z=1,原方程的一组解为(2,0,1).
当k≥1时,对式⑥两边模4得![]()
于是,y是偶数.设![]()
此时,再对式⑥两边模8得![]()
于是,z为偶数.设![]()
于是,式⑥变为![]()
结合(1)的结论知![]() 于是,
于是,![]() ,矛盾.
,矛盾.
故(![]() ,y,z)=(1,0,0),(1,1,0),(2,1,0),(3,2,0),(4,l,1),(2,0,1).
,y,z)=(1,0,0),(1,1,0),(2,1,0),(3,2,0),(4,l,1),(2,0,1).

 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案【题目】水稻是人类重要的粮食作物之一,耕种与食用的历史都相当悠久,日前我国南方农户在播种水稻时一般有直播、撒酒两种方式.为比较在两种不同的播种方式下水稻产量的区别,某市红旗农场于2019年选取了200块农田,分成两组,每组100块,进行试验.其中第一组采用直播的方式进行播种,第二组采用撒播的方式进行播种.得到数据如下表:
产量(单位:斤) 播种方式 | [840,860) | [860,880) | [880,900) | [900,920) | [920,940) |
直播 | 4 | 8 | 18 | 39 | 31 |
散播 | 9 | 19 | 22 | 32 | 18 |
约定亩产超过900斤(含900斤)为“产量高”,否则为“产量低”
(1)请根据以上统计数据估计100块直播农田的平均产量(同一组中的数据用该组区间的中点值为代表)
(2)请根据以上统计数据填写下面的2×2列联表,并判断是否有99%的把握认为“产量高”与“播种方式”有关?
产量高 | 产量低 | 合计 | |
直播 | |||
散播 | |||
合计 |
附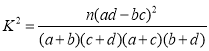 :
:
P(K2≥k0) | 0.10 | 0.010 | 0.001 |
k0 | 2.706 | 6.635 | 10.828 |
【题目】某公交公司为了方便市民出行、科学规划车辆投放,在一个人员密集流动地段增设一个起点站,为研究车辆发车间隔时间![]() (分钟)与乘客等候人数
(分钟)与乘客等候人数![]() (人)之间的关系,经过调查得到如下数据:
(人)之间的关系,经过调查得到如下数据:
间隔时间 |
|
|
|
|
|
|
等候人数 |
|
|
|
|
|
|
调查小组先从这![]() 组数据中选取
组数据中选取![]() 组数据求线性回归方程,再用剩下的
组数据求线性回归方程,再用剩下的![]() 组数据进行检验.检验方法如下:先用求得的线性回归方程计算间隔时间对应的等候人数
组数据进行检验.检验方法如下:先用求得的线性回归方程计算间隔时间对应的等候人数![]() ,再求
,再求![]() 与实际等候人数
与实际等候人数![]() 的差,若差值的绝对值不超过
的差,若差值的绝对值不超过![]() ,则称所求线性回归方程是“恰当回归方程”.
,则称所求线性回归方程是“恰当回归方程”.
(1)从这![]() 组数据中随机选取
组数据中随机选取![]() 组数据后,求剩下的
组数据后,求剩下的![]() 组数据的间隔时间之差大于
组数据的间隔时间之差大于![]() 的概率;
的概率;
(2)若选取的是后面![]() 组数据,求
组数据,求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,并判断此方程是否是“恰当回归方程”;
,并判断此方程是否是“恰当回归方程”;
(3)在(2)的条件下,为了使等候的乘客不超过![]() 人,则间隔时间最多可以设置为多少分钟?(精确到整数)
人,则间隔时间最多可以设置为多少分钟?(精确到整数)
参考公式: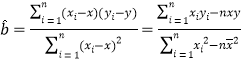 ,
,![]() .
.