Question

【题目】设函数f（x）=x2﹣2|x|﹣1（﹣3≤x≤3），
（1）画出这个函数的图象；
（2）指出函数f（x）的单调区间，并说明在各个单调区间上f（x）是增函数还是减函数；
（3）求函数的值域．

Answer 1

【答案】
（1）解：当x≥0时，f（x）=x2﹣2x﹣1=（x﹣1）2﹣2，

当x＜0时，f（x）=x2+2x﹣1=（x+1）2﹣2，

根据二次函数的作图方法，可得函数图象如图

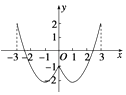
（2）解：函数f（x）的单调区间为

[﹣3，﹣1），[﹣1，0），[0，1），[1，3]．

f（x）在区间[﹣3，﹣1）和[0，1）上为减函数，

在[﹣1，0），[1，3]上为增函数

（3）解：当x≥0时，函数f（x）=（x﹣1）2﹣2的最小值为﹣2，

最大值为f（3）=2；

当x＜0时，函数f（x）=（x+1）2﹣2的最小值为﹣2，

最大值为f（﹣3）=2．

故函数f（x）的值域为[﹣2，2]

【解析】（1）化为分段函数，根据二次函数的作图方法，可得函数图象如图．（2）由图象可得函数得到f（x）的单调区间，（3）由图象可得函数的值域．