题目内容
已知
，且
为幂函数，则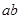
的最大值为
A． | B． | C． | D． |
A
解析试题分析：由于已知中给定是幂函数，则说明a+2b=1,同时
因此那么由均值不等式
，那么可知
当且仅当
时取得等号，故选A.
考点：本试题考查了幂函数的概念运用。
点评：根据已知的幂函数得到a,b的关系式，进而利用函数的单调性的性质或者均值不等式来求解得到最大值。这是求最值的一般思路，先化简为一个元的函数，或者构造定值，求解最值。属于中档题。
练习册系列答案
相关题目
已知函数f(x)＝
则函数f(x)的零点个数为( )
| A．1 | B．2 | C．3 | D．4 |
若函数
有两个不同的零点
，且
，那么在
两个函数值中 ( )
| A．只有一个小于1 | B．至少有一个小于1 |
| C．都小于1 | D．可能都大于1 |
当
时，
（
）,则
的取值范围是( )
A．（０， ） | B．（，１） | C．（１， ） | D．（，２） |
函数
，满足
的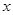
的取值范围（ ）
A． | B． | C． | D． |
已知
，若方程
存在三个不等的实根
，则
的取值范围是
A． | B． | C． | D． |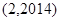
设函数
的值域为R，则常数
的取值范围是
A． | B． | C． | D． |
的零点个数是（ ）
| A．0个 | B．1个 | C．2个 | D．3个 |
不等式
对
恒成立，则
的取值范围是（ ）
A． | B． | C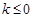． | D． |