题目内容
若函数 有两个不同的零点
有两个不同的零点 ,且
,且 ,那么在
,那么在 两个函数值中 ( )
两个函数值中 ( )
| A.只有一个小于1 | B.至少有一个小于1 |
| C.都小于1 | D.可能都大于1 |
B
解析试题分析:由题意可得函数f(x)=(x-x1)(x-x2),∴f(1)=(1-x1)(1-x2)=(x1-1)(x2-1),f(3)=(3-x1)(3-x2),∴f(1)•f(3)=(x1-1)(x2-1)(3-x1)(3-x2)=(x1-1)(3-x1)(x2-1)(3-x2) < 。
。
即 f(1)•f(3)<1.故f(1),f(3)两个函数值中至少有一个小于1。
考点:一元二次方程根的分布问题。
点评:本题主要考查一元二次方程根的分布与系数的关系,本题解题的关键是把函数表示成两点式,利用基本不等式求出函数的最值,属于中档题.

练习册系列答案
相关题目
已知定义在R上的函数 满足
满足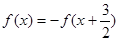 且
且 ,
, 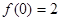 ,则
,则 等于( )
等于( )
A. | B. | C. | D. |
已知函数 若
若 则
则 的值为( )
的值为( )
A. | B. | C. | D. |
设函数 ,则满足
,则满足 的
的 的值是( )
的值是( )
| A.2 | B.16 | C.2或16 | D.-2或16 |
已知函数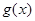 是
是 上的奇函数,且当
上的奇函数,且当 时
时 ,函数
,函数 若
若 >
> ,则实数
,则实数 的取值范围是
的取值范围是
A. | B. |
| C.(1,2) | D. |
函数f(x)= (a>0,a≠1)的图象恒过定点( ).
(a>0,a≠1)的图象恒过定点( ).
A. | B. | C. | D. |
已知定义域为 的函数
的函数 满足:
满足: ,且
,且 ,当
,当 时,
时, ,则
,则 等于
等于
A. | B. | C. | D. |
已知 ,且
,且 为幂函数,则
为幂函数,则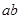 的最大值为
的最大值为
A. | B. | C. | D. |
若 ,则
,则 的解集为 ( )
的解集为 ( )
A. | B. | C. | D. |