题目内容
当 时,
时, (
( ),则
),则 的取值范围是( )
的取值范围是( )
A.(0, ) ) | B.( ,1) ,1) | C.(1, ) ) | D.( ,2) ,2) |
B
解析试题分析:根据已知条件,那么当 时,
时, ,那么结合指数函数与对数函数的图像和性质可知,只有底数0<a<1时,能满足题意,但是要注意定义域的限制,假设在x=
,那么结合指数函数与对数函数的图像和性质可知,只有底数0<a<1时,能满足题意,但是要注意定义域的限制,假设在x=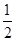 处函数值相等,则有
处函数值相等,则有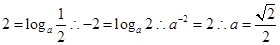 ,那么对数函数当底数越大,则图像越来越远离于y轴,这样依然能满足题意,故参数
,那么对数函数当底数越大,则图像越来越远离于y轴,这样依然能满足题意,故参数 的取值范围是(
的取值范围是( ,1),选B.
,1),选B.
考点:本试题考查了不等式的知识。
点评:解决该试题的关键是利用给定的不等式,结合函数的图像来分析,利用相交时的边界点处函数值相等来分析底数的值,同时结合对数函数的图像的变化与底数的关系来得到结论,属于中档题。

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
已知函数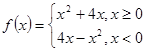 ,若
,若 ,则实数
,则实数 的取值范围( )
的取值范围( )
A. | B. | C. | D.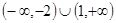 |
设函数 ,则满足
,则满足 的
的 的值是( )
的值是( )
| A.2 | B.16 | C.2或16 | D.-2或16 |
函数f(x)= (a>0,a≠1)的图象恒过定点( ).
(a>0,a≠1)的图象恒过定点( ).
A. | B. | C. | D. |
已知定义域为 的函数
的函数 满足:
满足: ,且
,且 ,当
,当 时,
时, ,则
,则 等于
等于
A. | B. | C. | D. |
二次函数 的图象的对称轴为
的图象的对称轴为 ,则当
,则当 时,
时, 的值为( )
的值为( )
A. | B.1 | C.17 | D.25 |
已知 ,且
,且 为幂函数,则
为幂函数,则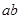 的最大值为
的最大值为
A. | B. | C. | D. |
 满足
满足 ,下列不等式中正确的是( )
,下列不等式中正确的是( )
A. | B. | C. | D. |
函数 的零点所在的大致区间是( )
的零点所在的大致区间是( )
A. | B. | C. 和 和 | D. |