题目内容
【题目】已知函数![]() ,
,![]() .
.
(1)若![]() ,
,![]() 在
在![]() 上恒成立,求
上恒成立,求![]() 的取值范围;
的取值范围;
(2)设数列![]() ,
,![]() 为数列
为数列![]() 的前
的前![]() 项和,求证:
项和,求证:![]() ;
;
(3)当![]() 时,设函数
时,设函数![]() 的图象
的图象![]() 与函数
与函数![]() 的图象
的图象![]() 交于点
交于点![]() ,
,![]() ,过线段
,过线段![]() 的中点
的中点![]() 作
作![]() 轴的垂线分别交
轴的垂线分别交![]() ,
,![]() 于点
于点![]() ,问是否存在点
,问是否存在点![]() ,使
,使![]() 在
在![]() 处的切线与
处的切线与![]() 在
在![]() 处的切线平行?若存在,求出
处的切线平行?若存在,求出![]() 的横坐标;若不存在,请说明理由.
的横坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)详见解析;(3)不存在.
;(2)详见解析;(3)不存在.
【解析】
(1)当![]() 时,
时,![]() ,即
,即![]() ,设
,设![]() ,利用导数得到函数的单调性与最值,即可求得求解;
,利用导数得到函数的单调性与最值,即可求得求解;
(2)由(1)得![]() 在
在![]() 上恒成立,令
上恒成立,令![]() 得
得![]() ,则
,则![]() ,即可作出证明;
,即可作出证明;
(3)![]() ,设点
,设点![]() 的坐标是
的坐标是![]() ,
,![]() ,得到
,得到![]() 在点
在点![]() 处的切线斜率为
处的切线斜率为![]() ,
,![]() 在点
在点![]() 处的切线斜率为
处的切线斜率为![]() ,根据
,根据![]() ,即
,即![]() ,整理得
,整理得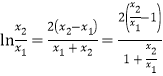 ,设
,设![]() ,得到函数
,得到函数![]() ,
,![]() ,再令
,再令![]() ,
,![]() ,利用导数得到
,利用导数得到![]() 的单调性和最值,即可求解.
的单调性和最值,即可求解.
(1)当![]() 时,
时,![]() ,即
,即![]() ,
,
设![]() ,则
,则![]() .
.
若![]() ,显然不满足题意;
,显然不满足题意;
若![]() ,则
,则![]() 时,
时,![]() 恒成立,
恒成立,
所以![]() 在
在![]() 上为减函数,有
上为减函数,有![]() 在
在![]() 上恒成立;
上恒成立;
若![]() ,则
,则![]() 时,
时,![]() ,
,![]() 时
时![]() ,
,
所以![]() 在
在![]() 上单调递增.
上单调递增.
∵![]() ,∴
,∴![]() 时,
时,![]() ,不满足题意.
,不满足题意.
综上,![]() 时
时![]() 在
在![]() 上恒成立.
上恒成立.
(2)由(1)得![]() 在
在![]() 上恒成立,
上恒成立,
令![]() 有
有![]() ,
,![]() ,
,
则![]() ,
,
∴![]()
![]() ,
,
即![]() .
.
(3)![]() ,设点
,设点![]() 的坐标是
的坐标是![]() ,
,![]() ,且
,且![]() ,
,
则点![]() 的中点坐标为
的中点坐标为![]() ,
,
![]() 在点
在点![]() 处的切线斜率为
处的切线斜率为![]() ,
,
![]() 在点
在点![]() 处的切线斜率为
处的切线斜率为![]() ,
,
假设![]() 在点
在点![]() 处的切线与
处的切线与![]() 在点
在点![]() 处的切线平行,则
处的切线平行,则![]() ,即
,即![]() .
.
所以![]()
![]()
![]() ,
,
所以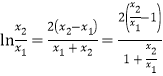 .
.
设![]() ,则
,则![]() ,
,![]() . ①
. ①
令![]() ,
,![]() ,则
,则![]() .
.
因为![]() ,所以
,所以![]() ,所以
,所以![]() 在
在![]() 上单调递增.
上单调递增.
故![]() ,则
,则![]() .
.
这与①矛盾,假设不成立.
故不存在点![]() ,使
,使![]() 在点
在点![]() 处的切线与
处的切线与![]() 在点
在点![]() 处的切线平行.
处的切线平行.

【题目】某省级示范高中高三年级对考试的评价指标中,有“难度系数”“区分度”和“综合”三个指标,其中,难度系数![]() ,区分度
,区分度![]() ,综合指标
,综合指标![]() .以下是高三年级 6 次考试的统计数据:
.以下是高三年级 6 次考试的统计数据:
i | 1 | 2 | 3 | 4 | 5 | 6 |
难度系数 xi | 0.66 | 0.72 | 0.73 | 0.77 | 0.78 | 0.84 |
区分度 yi | 0.19 | 0.24 | 0.23 | 0.23 | 0.21 | 0.16 |
(I) 计算相关系数![]() ,若
,若![]() ,则认为
,则认为![]() 与
与![]() 的相关性强;通过计算相关系数
的相关性强;通过计算相关系数![]() ,能否认为
,能否认为![]() 与
与![]() 的相关性很强(结果保留两位小数)?
的相关性很强(结果保留两位小数)?
(II) 根据经验,当![]() 时,区分度
时,区分度![]() 与难度系数
与难度系数![]() 的相关性较强,从以上数据中剔除(0.7,0.8)以外的
的相关性较强,从以上数据中剔除(0.7,0.8)以外的![]() 值,即
值,即![]() .
.
(i) 写出剩下 4 组数据的线性回归方程(![]() 保留两位小数);
保留两位小数);
(ii) 假设当![]() 时,
时,![]() 与
与![]() 的关系依从(i)中的回归方程,当
的关系依从(i)中的回归方程,当![]() 为何值时,综合指标
为何值时,综合指标![]() 的值最大?
的值最大?
参考数据:
![]()
参考公式:
相关系数
回归方程中斜率和截距的最小二乘估计公式为

【题目】下表是20个国家和地区的二氧化碳排放总量及人均二氧化碳排放量.
国家和地区 | 排放总量/千吨 | 人均排放量/吨 | 国家和地区 | 排放总量/千吨 | 人均排放量/吨 | |
A | 10330000 | 7.4 | K | 480000 | 2.0 | |
B | 5300000 | 16.6 | L | 480000 | 7.5 | |
C | 3740000 | 7.3 | M | 470000 | 3.9 | |
D | 2070000 | 1.7 | N | 410000 | 5.3 | |
E | 1800000 | 12.6 | O | 390000 | 16.9 | |
F | 1360000 | 10.7 | P | 390000 | 6.4 | |
G | 840000 | 10.2 | Q | 370000 | 5.7 | |
H | 630000 | 12.7 | R | 330000 | 6.2 | |
I | 550000 | 15.7 | S | 320000 | 6.2 | |
J | 510000 | 2.6 | T | 490000 | 16.6 |
(1)这20个国家和地区人均二氧化碳排放量的中位数是多少?
(2)针对这20个国家和地区,请你找出二氧化碳排放总量较少的前15%的国家和地区.