题目内容
【题目】从某小学随机抽取100名同学,将他们的身高(单位:厘米)数据绘制成频率分布直方图(如图),
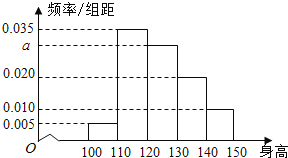
(1)由图中数据求a的值;
(2)若要从身高在[120,130),[130,140),[140,150]三组内的学生中,用分层抽样的方法选取18人参加一项活动,则从身高在[140,150]内的学生中选取的人数应为多少?
(3)估计这所小学的小学生身高的众数,中位数(保留两位小数)及平均数.
【答案】(1)a=0.030;(2)3人;(3)众数115cm,中位数123.33cm,平均数124.5cm
【解析】
(1)根据频率和为1,求出[120,130)频率,再除以10,即为所求的值;
(2)先求出三组的人数,根据分层抽样按比例分配,将18人按比例分配,即可求解;
(3)根据直方图,频率最大组的中间值,为众数;从左到右求出频率和为0.5所在的组,再求出在该组所占的比例,即可求出中位数;根据平均数的公式,即可求解.
(1)因为直方图中的各个矩形的面积之和为1,
所以有10×(0.005+0.035+a+0.020+0.010)=1,
解得a=0.030;
(2)由直方图知,三个区域内的学生总数为
100×10×(0.030+0.020+0.010)=60人,
其中身高在[140,150]内的学生人数为10人,
所以从身高在[140,150]范围内抽取的学生人数为
![]() 10=3人;
10=3人;
(3)根据频率分布直方图知,身高在[110,120)内的小矩形图最高,
所以该组数据的众数为![]() 115cm;
115cm;
又0.005×10+0.035×10=0.4<0.5,
0.4+0.030×10=0.7>0.5,
所以中位数在[120,130)内,
则中位数为![]() ;
;
根据频率分布直方图,计算平均数为
105×0.05+115×0.35+125×0.3+135×0.2+145×0.1=124.5cm.

 名校课堂系列答案
名校课堂系列答案【题目】计划在某水库建一座至多安装3台发电机的水电站,过去50年的水文资料显示,水库年入流量![]() (年入流量:一年内上游来水与库区降水之和.单位:亿立方米)都在40以上.其中,不足80的年份有10年,不低于80且不超过120的年份有35年,超过120的年份有5年.将年入流量在以上三段的频率作为相应段的概率,并假设各年的年入流量相互独立.
(年入流量:一年内上游来水与库区降水之和.单位:亿立方米)都在40以上.其中,不足80的年份有10年,不低于80且不超过120的年份有35年,超过120的年份有5年.将年入流量在以上三段的频率作为相应段的概率,并假设各年的年入流量相互独立.
(1)求未来4年中,至多1年的年入流量超过120的概率;
(2)水电站希望安装的发电机尽可能运行,但每年发电机最多可运行台数受年入流量![]() 限制,并有如下关系:
限制,并有如下关系:
年入流量 |
|
|
|
发电量最多可运行台数 | 1 | 2 | 3 |
若某台发电机运行,则该台年利润为5000万元;若某台发电机未运行,则该台年亏损800万元,欲使水电站年总利润的均值达到最大,应安装发电机多少台?
【题目】“大众创业,万众创新”是李克强总理在本届政府工作报告中向全国人民发出的口号.某生产企业积极响应号召,大力研发新产品,为了对新研发的一批产品进行合理定价,将该产品按事先拟定的价格进行试销,得到一组销售数据![]() (
(![]() =1,2,…,6),如表所示:
=1,2,…,6),如表所示:
试销单价 | 4 | 5 | 6 | 7 | 8 | 9 |
产品销量 | q | 84 | 83 | 80 | 75 | 68 |
已知![]() .
.
(Ⅰ)求出![]() 的值;
的值;
(Ⅱ)已知变量![]() 具有线性相关关系,求产品销量
具有线性相关关系,求产品销量![]() (件)关于试销单价
(件)关于试销单价![]() (元)的线性回归方程
(元)的线性回归方程![]() ;
;
(参考公式:线性回归方程中![]() ,
,![]() 的最小二乘估计分别为
的最小二乘估计分别为 ,
,![]() )
)