题目内容
(满分13分)已知椭圆中心在原点,焦点在x轴上,离心率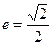 ,点
,点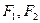 分别为椭圆的左、右焦点,过右焦点
分别为椭圆的左、右焦点,过右焦点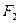 且垂直于长轴的弦长为
且垂直于长轴的弦长为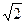
⑴ 求椭圆的标准方程;
⑵ 过椭圆的左焦点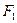 作直线
作直线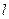 ,交椭圆于
,交椭圆于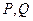 两点,若
两点,若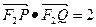 ,求直线
,求直线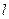 的倾斜角。
的倾斜角。
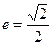 ,点
,点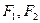 分别为椭圆的左、右焦点,过右焦点
分别为椭圆的左、右焦点,过右焦点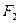 且垂直于长轴的弦长为
且垂直于长轴的弦长为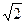
⑴ 求椭圆的标准方程;
⑵ 过椭圆的左焦点
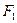 作直线
作直线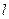 ,交椭圆于
,交椭圆于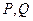 两点,若
两点,若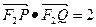 ,求直线
,求直线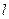 的倾斜角。
的倾斜角。⑴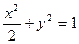
⑵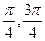
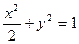
⑵
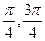
(1)略
(2)略
(2)略

练习册系列答案
相关题目
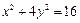 有相同焦点,且椭圆C上一点P到两焦点的距离之和等于
有相同焦点,且椭圆C上一点P到两焦点的距离之和等于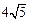 ,求椭圆C的标准方程;
,求椭圆C的标准方程; 的长轴长为4.
的长轴长为4.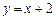 相切,求椭圆焦点坐标;
相切,求椭圆焦点坐标; ,求椭圆的方程.
,求椭圆的方程.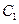 的方程为
的方程为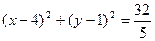 ,椭圆
,椭圆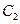 的方程
的方程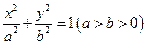 ,且离心率为
,且离心率为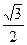 ,如果
,如果 两点,且线段
两点,且线段 恰为圆
恰为圆 ,椭圆上是否存在点
,椭圆上是否存在点 ,使得
,使得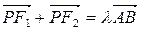 ,如果存在,请求点
,如果存在,请求点
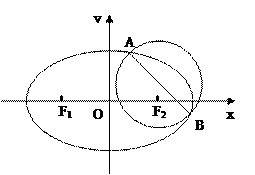
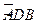 为半圆,AB为半圆直径,O为半圆圆心,且OD⊥AB,Q为线段OD的中点,已知|AB|=4,曲线C过Q点,动点P在曲线C上运动且保持|PA|+|PB|的值不变.
为半圆,AB为半圆直径,O为半圆圆心,且OD⊥AB,Q为线段OD的中点,已知|AB|=4,曲线C过Q点,动点P在曲线C上运动且保持|PA|+|PB|的值不变.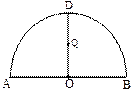
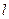 使
使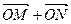 与
与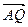 平行,若平行,求出直线
平行,若平行,求出直线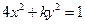 的曲线是焦点在
的曲线是焦点在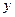 轴上的椭圆,则
轴上的椭圆,则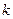 的取值范围是
的取值范围是 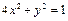 及直线
及直线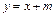 ,当直线被椭圆截得的弦最长时的直线方程为
,当直线被椭圆截得的弦最长时的直线方程为
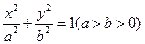 的长轴,短轴端点分别是A,B,从椭圆上一点M向x轴作垂线,恰好通过椭圆的左焦点,向量
的长轴,短轴端点分别是A,B,从椭圆上一点M向x轴作垂线,恰好通过椭圆的左焦点,向量 与
与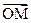 是共线向量
是共线向量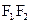 分别是左右焦点,求
分别是左右焦点,求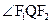 的取值范围
的取值范围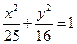 上一点
上一点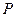 到左准线的距离为10,
到左准线的距离为10,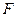 是该椭圆的左焦点,若点
是该椭圆的左焦点,若点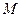 满足
满足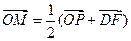 ,则
,则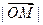 = .
= .