题目内容
6.已知双曲线x2-$\frac{{y}^{2}}{4}$=1,试问:是否存在过点A(2,1)的直线与双曲线交于相异两点P、Q.且点A平分线段PQ?分析 假设存在这样的直线,设出P,Q的坐标,代入双曲线方程,两式相减,根据中点的坐标可知x1+x2和y1+y2的值,进而求得直线PQ的斜率,根据点斜式求得直线的方程,再加以检验即可判断.
解答 解:假设存在这样的直线,点A平分线段PQ.
设P(x1,y1),Q(x2,y2),
则x1+x2=4,y1+y2=2,
∵4x12-y12=4,4x22-y22=4,
∴16(x1-x2)-2(y1-y2)=0,
∴kPQ=8,
∴直线的方程为y-1=8(x-2),即8x-y-15=0.
联立双曲线方程,消去y,可得60x2-240x+229=0,
由判别式为2402-4×60×229>0,
可得存在这样的直线,点A平分线段PQ.
点评 涉及弦长的中点问题,常用“点差法”设而不求,将弦所在直线的斜率、弦的中点坐标联系起来,相互转化.

练习册系列答案
相关题目
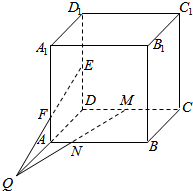 如图,在正方体ABCD-A1B1C1D1中,点M,N,E,F分别是CD、AB、DD1、AA1上的点,若MN与EF交于点Q,求证:D,A,Q三点共线.
如图,在正方体ABCD-A1B1C1D1中,点M,N,E,F分别是CD、AB、DD1、AA1上的点,若MN与EF交于点Q,求证:D,A,Q三点共线.