题目内容
已知函数f(x)是R上的增函数,设F(x)=f(x)-f(a-x).(1)用函数单调性定义证明F(x)是R上的增函数;
(2)求证:函数y=F(x)的图像关于点(![]() ,0)成中心对称图形.
,0)成中心对称图形.
思路分析:(1)证明函数F(x)的单调性要用到函数f(x)的单调性;(2)证明函数y=F(x)的图像上任一点关于点(![]() ,0)的对称点也在函数y=F(x)图像上即可.
,0)的对称点也在函数y=F(x)图像上即可.
解:(1)设x1、x2∈R,且x1<x2,则
F(x1)-F(x2)=[f(x1)-f(a-x1)]-[f(x2)-f(a-x2)]
=[f(x1)-f(x2)]+[f(a-x2)-(a-x1)].
又∵函数f(x)是R上的增函数,x1<x2,
∴a-x2<a-x1.
∴f(x1)<f(x2).∴f(a-x2)<f(a-x1).
∴[f(x1)-f(x2)]+[f(a-x2)-f(a-x1)]<0.
∴F(x1)<F(x2).
∴F(x)是R上的增函数.
(2)设点M(x0,F(x0))是函数F(x)图像上任意一点,则点M(x0,F(x0))关于点(![]() ,0)的对称点M′(a-x0,-F(x0)).
,0)的对称点M′(a-x0,-F(x0)).
又∵F(a-x0)=f(a-x0)-f[a-(a-x0)]
=f(a-x0)-f(x0)
=-[f(x0)-f(a-x0)]
=-F(x0),
∴点M′(a-x0,-F(x0))也在函数F(x)图像上.
又∵点M(x0,F(x0))是函数F(x)图像上任意一点,
∴函数y=F(x)的图像关于点(![]() ,0)成中心对称图形.
,0)成中心对称图形.

练习册系列答案
相关题目
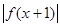 <1
<1 的解集的补集是( )
的解集的补集是( )