题目内容
已知函数f(x)是R上的增函数,a、b∈R.(1)证明命题“如果a+b≥0,那么f(a)+f(b)≥f(-a)+f(-b)成立”;
(2)判断(1)中命题的逆命题是否成立,并证明你的结论.
(1)证明:当a+b≥0![]() a≥-b
a≥-b![]() b≥-a,且f(x)是R上的增函数,
b≥-a,且f(x)是R上的增函数,
∴f(a)≥f(-b),f(b)≥f(-a).
∴f(a)+f(b)≥f(-a)+f(-b).
(2)解析:逆命题“如果f(a)+f(b)≥f(-a)+f(-b),则a+b≥0”是正确的,下面用反证法证明.
若a+b<0,则a<-b,b<-a.又f(x)是R上的增函数,
∴f(a)+f(b)<f(-a)+f(-b),这与条件f(a)+f(b)≥f(-a)+f(-b)矛盾.
∴a+b≥0成立.

练习册系列答案
相关题目
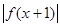 <1
<1 的解集的补集是( )
的解集的补集是( )