题目内容
已知函数 ,其中
,其中 ,
, 为自然对数的底数.
为自然对数的底数.
(Ⅰ)设 是函数
是函数 的导函数,求函数
的导函数,求函数 在区间
在区间 上的最小值;
上的最小值;
(Ⅱ)若 ,函数
,函数 在区间
在区间 内有零点,求
内有零点,求 的取值范围
的取值范围
(Ⅰ)当 时,
时,  ;当
;当 时,
时,  ;
;
当 时,
时,  .(Ⅱ)
.(Ⅱ) 的范围为
的范围为 .
.
解析试题分析:(Ⅰ)易得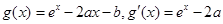 ,再对分
,再对分 情况确定
情况确定 的单调区间,根据
的单调区间,根据 在
在 上的单调性即可得
上的单调性即可得 在
在 上的最小值.(Ⅱ)设
上的最小值.(Ⅱ)设 为
为 在区间
在区间 内的一个零点,注意到
内的一个零点,注意到 .联系到函数的图象可知,导函数
.联系到函数的图象可知,导函数 在区间
在区间 内存在零点
内存在零点 ,
, 在区间
在区间 内存在零点
内存在零点 ,即
,即 在区间
在区间 内至少有两个零点. 由(Ⅰ)可知,当
内至少有两个零点. 由(Ⅰ)可知,当 及
及 时,
时, 在
在 内都不可能有两个零点.所以
内都不可能有两个零点.所以 .此时,
.此时, 在
在 上单调递减,在
上单调递减,在 上单调递增,因此
上单调递增,因此 ,且必有
,且必有 .由
.由 得:
得: ,代入这两个不等式即可得
,代入这两个不等式即可得 的取值范围.
的取值范围.
试题解答:(Ⅰ)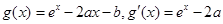
①当 时,
时, ,所以
,所以 .
.
②当 时,由
时,由 得
得 .
.
若 ,则
,则 ;若
;若 ,则
,则 .
.
所以当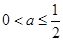 时,
时, 在
在 上单调递增,所以
上单调递增,所以 .
.
当 时,
时, 在
在 上单调递减,在
上单调递减,在 上单调递增,所以
上单调递增,所以 .
.
当 时,
时, 在
在 上单调递减,所以
上单调递减,所以 .
.
(Ⅱ)设 为
为 在区间
在区间 内的一个零点,则由
内的一个零点,则由 可知,
可知, 在区间
在区间 上不可能单调递增,也不可能单调递减.
上不可能单调递增,也不可能单调递减.
则 不可能恒为正,也不可能恒为负.
不可能恒为正,也不可能恒为负.
故 在区间
在区间 内存在零点
内存在零点 .
.
同理 在区间
在区间 内存在零点
内存在零点 .
.
所以 在区间
在区间 内至少有两个零点.
内至少有两个零点.
由(Ⅰ)知,当 时,
时, 在
在 上单调递增,故
上单调递增,故 在
在 内至多有一个零点.
内至多有一个零点.
当
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 上函数
上函数 为奇函数.
为奇函数. 的值;
的值; 的值域.
的值域.
 在区间
在区间 上单调递减,求
上单调递减,求 的取值范围;
的取值范围; 时,
时, 恒成立,求
恒成立,求 的最大值及此时
的最大值及此时 为偶函数,曲线
为偶函数,曲线 过点
过点 ,
,  .
. 有斜率为0的切线,求实数
有斜率为0的切线,求实数 的取值范围;
的取值范围; 时函数
时函数 (a是常数,a∈R)
(a是常数,a∈R) 的解集.
的解集. 恰有两个不同的零点,求a的取值范围.
恰有两个不同的零点,求a的取值范围. 的定义域为 .
的定义域为 .