题目内容
已知定义在区间(0,+∞)上的函数f(x)满足f(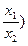 =f(x1)-f(x2),且当x>1时,f(x)<0.
=f(x1)-f(x2),且当x>1时,f(x)<0.
(1)求f(1)的值;
(2)判断f(x)的单调性;
(3)若f(3)=-1,解不等式f(|x|)<-2.
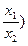 =f(x1)-f(x2),且当x>1时,f(x)<0.
=f(x1)-f(x2),且当x>1时,f(x)<0.(1)求f(1)的值;
(2)判断f(x)的单调性;
(3)若f(3)=-1,解不等式f(|x|)<-2.
(1)0(2)函数f(x)在区间(0,+∞)上是单调递减函数.(3)不等式的解集为{x|x>9或x<-9}
(1)令x1=x2>0,
代入得f(1)=f(x1)-f(x1)=0,故f(1)=0.
(2)任取x1,x2∈(0,+∞),且x1>x2,则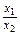 >1,
>1,
由于当x>1时,f(x)<0,
所以f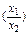 <0,即f(x1)-f(x2)<0,
<0,即f(x1)-f(x2)<0,
因此f(x1)<f(x2),
所以函数f(x)在区间(0,+∞)上是单调递减函数.
(3)由f(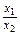 )=f(x1)-f(x2)得
)=f(x1)-f(x2)得
f(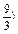 =f(9)-f(3),而f(3)=-1,所以f(9)=-2.
=f(9)-f(3),而f(3)=-1,所以f(9)=-2.
由于函数f(x)在区间(0,+∞)上是单调递减函数,
由f(|x|)<f(9),得|x|>9,∴x>9或x<-9.因此不等式的解集为{x|x>9或x<-9}.
代入得f(1)=f(x1)-f(x1)=0,故f(1)=0.
(2)任取x1,x2∈(0,+∞),且x1>x2,则
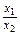 >1,
>1,由于当x>1时,f(x)<0,
所以f
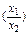 <0,即f(x1)-f(x2)<0,
<0,即f(x1)-f(x2)<0,因此f(x1)<f(x2),
所以函数f(x)在区间(0,+∞)上是单调递减函数.
(3)由f(
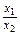 )=f(x1)-f(x2)得
)=f(x1)-f(x2)得f(
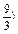 =f(9)-f(3),而f(3)=-1,所以f(9)=-2.
=f(9)-f(3),而f(3)=-1,所以f(9)=-2.由于函数f(x)在区间(0,+∞)上是单调递减函数,
由f(|x|)<f(9),得|x|>9,∴x>9或x<-9.因此不等式的解集为{x|x>9或x<-9}.

练习册系列答案
相关题目
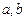 的值
的值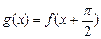 ,且
,且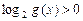 ,求
,求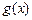 的单调区间
的单调区间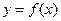 是奇函数,对于任意
是奇函数,对于任意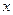 、
、 R都有
R都有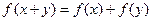 ,且当
,且当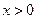 时,
时,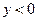 ,
,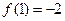 ,求函数
,求函数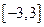 上的最大值和最小值.
上的最大值和最小值.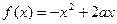 与
与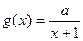 在区间
在区间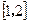 上都是减函数,则a的取值范围是( )
上都是减函数,则a的取值范围是( )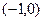
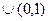 B
B 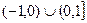 C
C 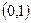 D
D 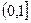
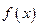 满足
满足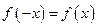 ,如果函数
,如果函数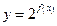 在
在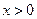 时是增函数,则在
时是增函数,则在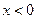 时,是增函数还是减函数?试证明.
时,是增函数还是减函数?试证明. ,都有
,都有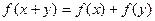 ,且
,且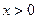 时,f(x)<0,f(1)=-2.
时,f(x)<0,f(1)=-2.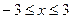 时,f(x)是否有最值?如果有求出最值;如果没有,说出理由.
时,f(x)是否有最值?如果有求出最值;如果没有,说出理由.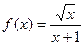 的最大值为 。
的最大值为 。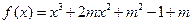 (其中
(其中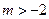 )
) ,求函数
,求函数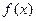 的单调区间及极小值;
的单调区间及极小值;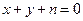 对任意的
对任意的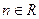 都不是曲线
都不是曲线 的切线,求
的切线,求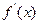 的最小值及实数
的最小值及实数 的取值范围.
的取值范围.