题目内容
8. 已知在△ABC中,∠C=90°,∠BAC与∠ABC的角平分线交于点I,求证:AI•BI=√2AB•r(r为内切圆I的半径).
已知在△ABC中,∠C=90°,∠BAC与∠ABC的角平分线交于点I,求证:AI•BI=√2AB•r(r为内切圆I的半径).
分析 先证明∠AIB=180°-∠BAI+∠ABI=135°,再利用等面积,即可证明结论.
解答 证明:∵AI和BI分别为角平分线
∴∠BAI=12∠BAC,∠ABI=12∠ABC
∵∠C=90°,
∴∠BAC+∠ACB=90°
∴∠BAI+∠ABI=45°
∴∠AIB=180°-∠BAI+∠ABI=135°
∴S△ABI=12AI•BI•sin135°
∵S△ABI=12AB•r
∴AI•BI•sin135°=AB•r
∴AI•BI=√2AB•r(r为内切圆I的半径).
点评 本题考查三角形的内切圆,考查等式的证明,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
18.函数y=11−√x+11+√x的导数y′=( )
| A. | 4x(1−x)2 | B. | -4x(1−x)2 | C. | 2(1−x)2 | D. | -2(1−x)2 |
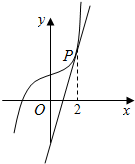 如图,已知函数f(x)=ax3+b,其图象上一点P处的切线为 l:y=4x-4,且点P的横坐标为2.
如图,已知函数f(x)=ax3+b,其图象上一点P处的切线为 l:y=4x-4,且点P的横坐标为2.