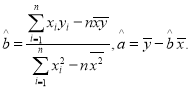题目内容
【题目】以任意方式把空间染成五种颜色(每点属于一色,每色的点都有).
(1)证明:存在一个平面,至少含有四种不同颜色的点;
(2)是否一定存在五色平面?
【答案】(1)见解析(2) 不一定.
【解析】
(1)若存在四色线![]() ,则含有
,则含有![]() 的平面即为所求.若存在三色线
的平面即为所求.若存在三色线![]() ,
,
则在线![]() 外可再取到一个第四色的点
外可再取到一个第四色的点![]() ,过点
,过点![]() 和线
和线![]() 的平面即为所求.
的平面即为所求.
假若任一直线上都不多于两色,为此,
用![]() 分别表示这五种颜色的点所构成的点集.取点
分别表示这五种颜色的点所构成的点集.取点![]() ,
,![]() ,过
,过![]() 的直线记为
的直线记为![]() ,则直线
,则直线![]() 上其余的点也属于
上其余的点也属于![]() 或
或![]() .
.
不妨设直线![]() 上有点
上有点![]() ,在空间分别取点
,在空间分别取点![]() 、
、![]() ,过
,过![]() 的平面记为
的平面记为![]() ,
,
则直线![]() 与平面
与平面![]() 有公共点
有公共点![]() .
.
若![]() ,则平面
,则平面![]() 即为所求(这时,平面
即为所求(这时,平面![]() 上含有
上含有![]() 四色).
四色).
若![]() ,在空间再取一点
,在空间再取一点![]() ,过点
,过点![]() 和直线
和直线![]() 作平面
作平面![]() ,
,
则平面![]() 和平面
和平面![]() 的交线为过
的交线为过![]() 的直线
的直线![]() .在平面
.在平面![]() 内,过点
内,过点![]() 的两条直线
的两条直线![]() 和
和![]() 中,
中,
至少有一条要与直线![]() 相交,不妨设
相交,不妨设![]() ,则点
,则点![]() 属于
属于![]() 或
或![]() .
.
于是,平面![]() 至少含有四色(或含
至少含有四色(或含![]() 或含
或含![]() ).
).
(2)不一定.例如,若将四面体![]() 的四个顶 点分别染成
的四个顶 点分别染成![]() 四色,
四色,
空间其余的点全染成![]() 色,这时,不存在五色平面.
色,这时,不存在五色平面.

 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案【题目】2020年新年伊始,新型冠状病毒来势汹汹,疫情使得各地学生在寒假结束之后无法返校,教育部就此提出了线上教学和远程教学,停课不停学的要求也得到了家长们的赞同.各地学校开展各式各样的线上教学,某地学校为了加强学生爱国教育,拟开设国学课,为了了解学生喜欢国学是否与性别有关,该学校对100名学生进行了问卷调查,得到如下列联表:
喜欢国学 | 不喜欢国学 | 合计 | |
男生 | 20 | 50 | |
女生 | 10 | ||
合计 | 100 |
(1)请将上述列联表补充完整,并判断能否在犯错误的概率不超过0.001的前提下认为喜欢国学与性别有关系?
(2)针对问卷调查的100名学生,学校决定从喜欢国学的人中按分层抽样的方法随机抽取6人成立国学宣传组,并在这6人中任选2人作为宣传组的组长,设这两人中女生人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
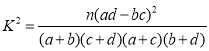 ,
,![]() .
.
【题目】为比较甲、乙两名蓝球运动员的近期竞技状态,选取这两名球员最近五场比赛的得分制成如图所示的茎叶图,有下列结论:
甲 | 乙 | |||||
9 | 8 | 5 | 2 | 8 | 9 | |
2 | 1 | 3 | 0 | 1 | 2 |
①甲最近五场比赛得分的中位数高于乙最近五场比赛得分的中位数.
②甲最近五场比赛得分的平均数低于乙最近五场比赛得分的平均数.
③从最近五场比赛的得分看,乙比甲更稳定.
④从最近五场比赛的得分看,甲比乙更稳定.
其中所有正确结论的编号为( )
A.①③B.①④C.②③D.②④
【题目】我市为改善空气环境质量,控制大气污染,政府相应出台了多项改善环境的措施.其中一项是为了减少燃油汽车对大气环境污染.从2018年起大力推广使用新能源汽车,鼓励市民如果需要购车,可优先考虑选用新能源汽车.政府对购买使用新能源汽车进行购物补贴,同时为了地方经济发展,对购买本市企业生产的新能源汽车比购买外地企业生产的新能源汽车补贴高.所以市民对购买使用本市企业生产的新能源汽车的满意度也相应有所提高.有关部门随机抽取本市本年度内购买新能源汽车的![]() 户,其中有
户,其中有![]() 户购买使用本市企业生产的新能源汽车,对购买使用新能源汽车的满意度进行调研,满意度以打分的形式进行.满分
户购买使用本市企业生产的新能源汽车,对购买使用新能源汽车的满意度进行调研,满意度以打分的形式进行.满分![]() 分,将分数按照
分,将分数按照![]() 分成5组,得如下频率分布直方图.
分成5组,得如下频率分布直方图.

(1)若本次随机抽取的样本数据中购买使用本市企业生产的新能源汽车的用户中有![]() 户满意度得分不少于
户满意度得分不少于![]() 分,把得分不少于
分,把得分不少于![]() 分为满意.根据提供的条件数据,完成下面的列联表.
分为满意.根据提供的条件数据,完成下面的列联表.
满意 | 不满意 | 总计 | |
购本市企业生产的新能源汽车户数 | |||
购外地企业生产的新能源汽车户数 | |||
总计 |
并判断是否有![]() 的把握认为购买使用新能源汽车的满意度与产地有关?
的把握认为购买使用新能源汽车的满意度与产地有关?
(2)以频率作为概率,政府对购买使用新能源汽车的补贴标准是:购买本市企业生产的每台补贴![]() 万元,购买外地企业生产的每台补贴
万元,购买外地企业生产的每台补贴![]() 万元.但本市本年度所有购买新能源汽车的补贴每台的期望值不超过
万元.但本市本年度所有购买新能源汽车的补贴每台的期望值不超过![]() 万元.则购买外地产的新能源汽车每台最多补贴多少万元?
万元.则购买外地产的新能源汽车每台最多补贴多少万元?
附:![]() ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|