题目内容
一名学生每天骑车上学,从他家到学校的途中有6个交通岗,假设他在各个交通岗遇到红灯的事件是相互独立的,并且概率都是 .
.
(1)设X为这名学生在途中遇到红灯的次数,求X的分布列;
(2)设Y为这名学生在首次停车前经过的路口数,求Y的概率分布;
(3)求这名学生在途中至少遇到一次红灯的概率.
 .
.(1)设X为这名学生在途中遇到红灯的次数,求X的分布列;
(2)设Y为这名学生在首次停车前经过的路口数,求Y的概率分布;
(3)求这名学生在途中至少遇到一次红灯的概率.
(1)X的分布列为
P(X=k)=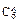
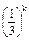 ·
·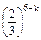 ,k=0,1,2,3,4,5,6.
,k=0,1,2,3,4,5,6.
(2)Y的概率分布为:
(3)0.912
P(X=k)=
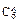
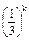 ·
·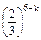 ,k=0,1,2,3,4,5,6.
,k=0,1,2,3,4,5,6.(2)Y的概率分布为:
| Y | 0 | 1 | 2 | 3 |
| P |  |  · ·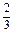 |  · ·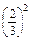 |  · ·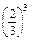 |
| Y | 4 | 5 | 6 |
| P |  · ·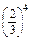 |  · ·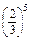 | 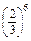 |
(3)0.912
(1)将通过每个交通岗看做一次试验,则遇到红灯的概率为 ,且每次试验结果是相互独立的,故X~B(6,
,且每次试验结果是相互独立的,故X~B(6, ), 2分
), 2分
所以X的分布列为
P(X=k)=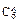
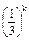 ·
·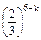 ,k=0,1,2,3,4,5,6. 5分
,k=0,1,2,3,4,5,6. 5分
(2)由于Y表示这名学生在首次停车时经过的路口数,显然Y是随机变量,其取值为0,1,2,3,4,5.
其中:{Y=k}(k=0,1,2,3,4,5)表示前k个路口没有遇上红灯,但在第k+1个路口遇上红灯,故各概率应按独立事件同时发生计算.
P(Y=k)=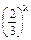 ·
· (k=0,1,2,3,4,5),
(k=0,1,2,3,4,5),
而{Y=6}表示一路没有遇上红灯,
故其概率为P(Y=6)=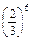 . 8分
. 8分
因此Y的概率分布为:
12分
(3)这名学生在途中至少遇到一次红灯的事件为
{X≥1}={X=1或X=2或…或X=6}, 14分
所以其概率为
P(X≥1)=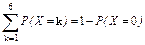 =1-
=1-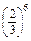 =
= ≈0.912. 16分
≈0.912. 16分
 ,且每次试验结果是相互独立的,故X~B(6,
,且每次试验结果是相互独立的,故X~B(6, ), 2分
), 2分所以X的分布列为
P(X=k)=
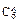
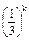 ·
·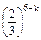 ,k=0,1,2,3,4,5,6. 5分
,k=0,1,2,3,4,5,6. 5分(2)由于Y表示这名学生在首次停车时经过的路口数,显然Y是随机变量,其取值为0,1,2,3,4,5.
其中:{Y=k}(k=0,1,2,3,4,5)表示前k个路口没有遇上红灯,但在第k+1个路口遇上红灯,故各概率应按独立事件同时发生计算.
P(Y=k)=
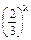 ·
· (k=0,1,2,3,4,5),
(k=0,1,2,3,4,5),而{Y=6}表示一路没有遇上红灯,
故其概率为P(Y=6)=
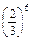 . 8分
. 8分因此Y的概率分布为:
| Y | 0 | 1 | 2 | 3 |
| P |  |  · ·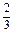 |  · ·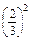 |  · ·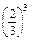 |
| Y | 4 | 5 | 6 |
| P |  · ·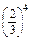 |  · ·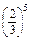 | 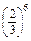 |
12分
(3)这名学生在途中至少遇到一次红灯的事件为
{X≥1}={X=1或X=2或…或X=6}, 14分
所以其概率为
P(X≥1)=
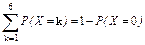 =1-
=1-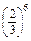 =
= ≈0.912. 16分
≈0.912. 16分
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目


 的概率分布.
的概率分布. 的概率分布如下表,且
的概率分布如下表,且
 ,则
,则 的值为( )
的值为( )

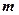

 ,求(1)油罐被引爆的概率;
,求(1)油罐被引爆的概率; :
:

 .
. ~
~ 且
且 ,
, ,则( )
,则( )


