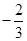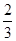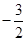题目内容
已知向量a=(cosα,-2),b=(sinα,1)且a∥b,则tan(α-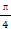 )等于( )
)等于( )
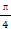 )等于( )
)等于( )| A.3 | B.-3 | C. | D.- |
B
选B.∵a=(cosα,-2), b=(sinα,1)且a∥b,
∴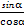 =
=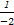 (经分析知cosα≠0),∴tanα=-
(经分析知cosα≠0),∴tanα=- .
.
∴tan(α- )=
)=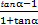 =
=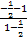 =-3,故选B.
=-3,故选B.
【方法技巧】解决向量与三角函数的综合题的方法
向量与三角函数的结合是近几年高考中出现较多的题目,解答此类题目的关键是根据条件将所给的向量问题转化为三角问题,然后借助三角恒等变换再根据三角求值、三角函数的性质、解三角形的问题来解决.
∴
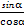 =
=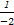 (经分析知cosα≠0),∴tanα=-
(经分析知cosα≠0),∴tanα=- .
.∴tan(α-
 )=
)=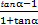 =
=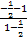 =-3,故选B.
=-3,故选B.【方法技巧】解决向量与三角函数的综合题的方法
向量与三角函数的结合是近几年高考中出现较多的题目,解答此类题目的关键是根据条件将所给的向量问题转化为三角问题,然后借助三角恒等变换再根据三角求值、三角函数的性质、解三角形的问题来解决.

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案
相关题目
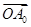 +
+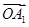 +…+OAn-1+
+…+OAn-1+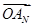 |等于( )
|等于( )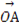 ⊥
⊥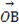 ,则向量
,则向量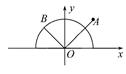
 ,
,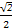 ,
, ,
,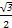 ,
,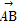 =a,
=a,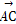 =b,对于平面ABC上任意一点O,动点P满足
=b,对于平面ABC上任意一点O,动点P满足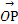 =
=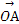 +λa+λb,则动点P的轨迹所过的定点为 .
+λa+λb,则动点P的轨迹所过的定点为 .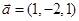 ,
,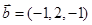 ;②
;②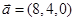 ,
,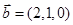 ;③
;③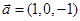 ,
,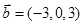 ;④
;④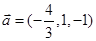 ,
,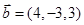
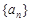 的前
的前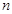 项和为
项和为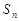 ,且
,且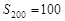 ,
,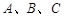 为平面内三点,点
为平面内三点,点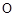 为平面外任意一点,若
为平面外任意一点,若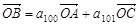 ,则
,则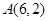 ,
,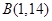 ,则与
,则与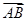 共线的单位向量为( )
共线的单位向量为( )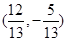 或
或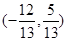
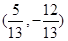
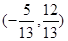 或
或 ,
,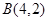 和向量
和向量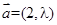 ,若
,若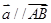 ,则实数
,则实数 的值为( )
的值为( )