题目内容
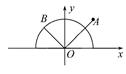
如图,已知点A(1,1)和单位圆上半部分上的动点B.且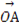 ⊥
⊥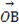 ,则向量
,则向量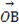 的坐标为( )
的坐标为( )
(A)(- ,
, ) (B)(-
) (B)(-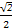 ,
,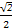 )
)
(C)(- ,
, ) (D)(-
) (D)(-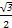 ,
,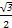 )
)
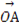 ⊥
⊥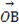 ,则向量
,则向量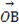 的坐标为( )
的坐标为( )
(A)(-
 ,
, ) (B)(-
) (B)(-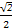 ,
,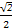 )
)(C)(-
 ,
, ) (D)(-
) (D)(-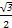 ,
,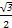 )
)B
依题意设B(cosθ,sinθ),0≤θ≤π.
则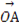 =(1,1),
=(1,1), =(cosθ,sinθ).
=(cosθ,sinθ).
因为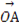 ⊥
⊥ ,所以
,所以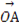 ·
· =0,
=0,
即cosθ+sinθ=0,
解得θ=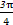 ,
,
所以 =(-
=(-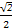 ,
,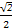 ).
).
【方法技巧】解题时引入恰当的参数θ是解题的关键,进而可利用三角函数的定义求得点B的坐标,可将问题转化为向量的坐标运算问题来解决.
则
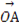 =(1,1),
=(1,1), =(cosθ,sinθ).
=(cosθ,sinθ).因为
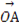 ⊥
⊥ ,所以
,所以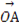 ·
· =0,
=0,即cosθ+sinθ=0,
解得θ=
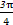 ,
,所以
 =(-
=(-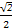 ,
,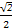 ).
).【方法技巧】解题时引入恰当的参数θ是解题的关键,进而可利用三角函数的定义求得点B的坐标,可将问题转化为向量的坐标运算问题来解决.

练习册系列答案
相关题目
 ,则向量
,则向量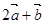 的坐标为( )
的坐标为( )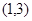
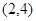
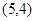
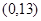
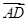 =x
=x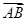 +y
+y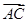 ,则x=________,y=________.
,则x=________,y=________.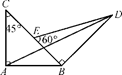
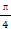 )等于( )
)等于( )
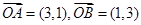 ,若
,若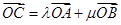 ,且
,且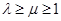 ,则用阴影表示
,则用阴影表示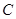 点所有可能的位置区域正确的是 ( )
点所有可能的位置区域正确的是 ( )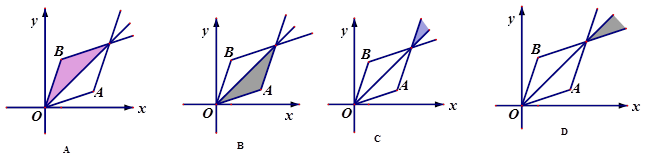
 与
与 共线且方向相反,则
共线且方向相反,则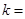 ( ).
( ).

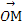 =2
=2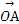 -
-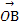 -
-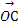
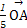 +
+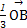 +
+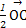
 +
+ +
+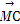 =0
=0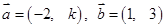 ,若
,若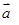 ⊥
⊥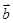 ,则实数
,则实数 .
.