题目内容
设点O在△ABC内部,且有
+2
+3
=
,则△AOB,△AOC,△BOC的面积比为( )
| OA |
| OB |
| OC |
| 0 |
| A.1:2:3 | B.3:2:1 | C.2:3:4 | D.4:3:2 |
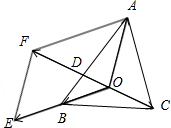
如图所示,
延长OB到点E,使得
=2
,
分别以
,
为邻边作平行四边形OAFE.
则
+2
=
+
=
,
∵
+2
+3
=
,
∴
=3
.
又
=2
,
∴
=2
.
∴
=
,
∴S△ABC=2S△AOB.
同理可得:S△ABC=3S△AOC,S△ABC=6S△BOC.
∴△AOB,△AOC,△BOC的面积比=3:2:1.
故选:B.
延长OB到点E,使得
| OE |
| OB |
分别以
| OA |
| OE |
则
| OA |
| OB |
| OA |
| OE |
| OF |
∵
| OA |
| OB |
| OC |
| 0 |
∴
| OF |
| OC |
又
| AF |
| OB |
∴
| DF |
| OD |
∴
| CO |
| OD |
∴S△ABC=2S△AOB.
同理可得:S△ABC=3S△AOC,S△ABC=6S△BOC.
∴△AOB,△AOC,△BOC的面积比=3:2:1.
故选:B.


练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

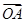 =(1,-2),
=(1,-2),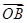 =(a,-1),
=(a,-1),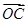 =(-b,0),a>0,b>0,O为坐标原点,若A、B、C三点共线,则
=(-b,0),a>0,b>0,O为坐标原点,若A、B、C三点共线,则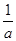 +
+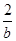 的最小值是________.
的最小值是________.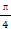 )等于( )
)等于( )
 与
与 均为单位向量,它们的夹角为
均为单位向量,它们的夹角为 ,那么
,那么 等于( )
等于( )


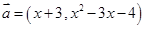 与
与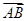 相等,其中
相等,其中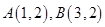 ,则
,则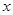 =_________.
=_________.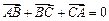 ;②若向量
;②若向量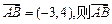 按向量
按向量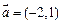 平移后的坐标仍是(-3,4);③“向量
平移后的坐标仍是(-3,4);③“向量 的方向相反”是“
的方向相反”是“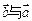 互为相反向量”的充分不必要条件;④已知点M是△ABC的重心,则
互为相反向量”的充分不必要条件;④已知点M是△ABC的重心,则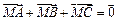 。
。