题目内容
(13分)已知,三棱锥P-ABC中,侧棱PC与底面成600的角,AB⊥AC,BP⊥AC,AB=4,AC=3.
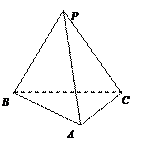
(1) 求证:截面ABP⊥底面ABC;(2)求三棱锥P-ABC的体积的最小值,及此时二面角A-PC-B的正切值.
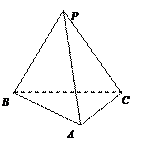
(1) 求证:截面ABP⊥底面ABC;(2)求三棱锥P-ABC的体积的最小值,及此时二面角A-PC-B的正切值.
 (2)
(2)
证(1):在三棱锥P-ABC中,∵ AB⊥AC, BP⊥AC, ∴AC⊥平面ABP,
∴平面ABP⊥平面ABC.
(2).作PH⊥面ABC于H, 则H在AB上,连CH,则∠HCP=600
当H与A重合时CH最短,棱锥的高PH=CHtan600= CH最短
CH最短
三棱锥P-ABC的体积V最小.此时,∠ACP=600, PH=AP=3
V=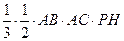
 ,∵
,∵ , AB⊥AC,∴
, AB⊥AC,∴ .
.
作 ,连
,连 ,由三垂线定理知
,由三垂线定理知 ,可知
,可知 是二面角A-PC-B的平面角.
是二面角A-PC-B的平面角.
在 中,PC=6,PA=
中,PC=6,PA= ,AD=
,AD= .在
.在 中可得,二面角A-PC-B的正切值为
中可得,二面角A-PC-B的正切值为
∴平面ABP⊥平面ABC.
(2).作PH⊥面ABC于H, 则H在AB上,连CH,则∠HCP=600
当H与A重合时CH最短,棱锥的高PH=CHtan600=
 CH最短
CH最短三棱锥P-ABC的体积V最小.此时,∠ACP=600, PH=AP=3

V=
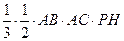
 ,∵
,∵ , AB⊥AC,∴
, AB⊥AC,∴ .
.作
 ,连
,连 ,由三垂线定理知
,由三垂线定理知 ,可知
,可知 是二面角A-PC-B的平面角.
是二面角A-PC-B的平面角.在
 中,PC=6,PA=
中,PC=6,PA= ,AD=
,AD= .在
.在 中可得,二面角A-PC-B的正切值为
中可得,二面角A-PC-B的正切值为

练习册系列答案
 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案
相关题目
 中,截面
中,截面 是正方形,则在下列命题中,错误的为( )
是正方形,则在下列命题中,错误的为( )

 ∥截面
∥截面
 与
与 所成的角为
所成的角为
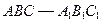 的各棱长都为
的各棱长都为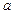 ,P为
,P为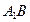 上的点,
上的点,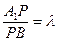 ,求
,求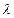 的值,使
的值,使
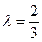 ,求二面角
,求二面角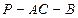 的大小
的大小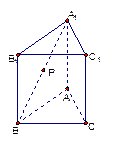
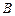 为等腰直角
为等腰直角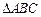 的直角顶点,
的直角顶点,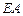 、
、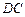 都垂直于
都垂直于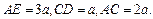

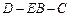 的大小;
的大小;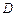 到平面
到平面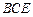 的距离;
的距离;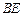 上是否存在一点
上是否存在一点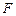 ,使得
,使得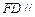 平面
平面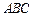 且
且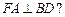 若存在,请指出
若存在,请指出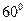 纬线长和赤道长的比值为( )
纬线长和赤道长的比值为( )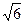 . (1)求证:AF//平面PCE;
. (1)求证:AF//平面PCE;
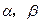 是两个不同的平面,m、n是平面
是两个不同的平面,m、n是平面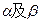 之外的两条不同直线,给出四个论断:(1)
之外的两条不同直线,给出四个论断:(1)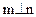 ,(2)
,(2)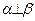 ,(3)
,(3)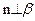 ,(4)
,(4)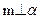 。以其中三个论断作为条件,余下一个论断为结论,写出你认为正确的一个命题___ _;
。以其中三个论断作为条件,余下一个论断为结论,写出你认为正确的一个命题___ _;