题目内容
10.计算:(1)${({\frac{13}{6}})^0}+{({\frac{1}{2}})^{-2}}-{({\frac{25}{4}})^{\frac{1}{2}}}+{({0.001})^{\frac{1}{3}}}$
(2)$lg4+lg25-{5^{{{log}_5}3}}+({log_2}9).({log_3}4)$.
分析 (1)利用有理指数幂的运算法则化简求解即可.
(2)利用对数的运算法则化简求解即可.
解答 解:(1)${({\frac{13}{6}})^0}+{({\frac{1}{2}})^{-2}}-{({\frac{25}{4}})^{\frac{1}{2}}}+{({0.001})^{\frac{1}{3}}}$
=1+4-$\frac{5}{2}$+0.1
=2.6.
(2)$lg4+lg25-{5^{{{log}_5}3}}+({log_2}9).({log_3}4)$
=2lg2+2lg5-3+$\frac{4lg3lg2}{lg2lg3}$
=3.
点评 本题考查有理指数幂以及对数的运算法则的应用,是基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.要得到函数g(x)=$sin(2x+\frac{π}{6})$,只需将f(x)=cos2x的图象( )
| A. | 左移$\frac{π}{3}$个单位 | B. | 右移$\frac{π}{3}$个单位 | C. | 左移$\frac{π}{6}$个单位 | D. | 右移$\frac{π}{6}$个单位 |
15.已知Sn是等差数列{an}的前n项和,若a1+a3+a5=3,则S5=( )
| A. | $\frac{5}{2}$ | B. | 5 | C. | 7 | D. | 9 |
19.如图所示是某一几何体的三视图,则这个几何体是( )
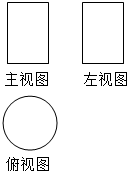

| A. | 圆柱体 | B. | 圆锥体 | C. | 正方体 | D. | 球体 |