题目内容
5.集合{1,2}的子集个数为4.分析 写出集合{1,2}的所有子集,从而得出该集合的子集个数.
解答 解:{1,2}的子集为:∅,{1},{2},{1,2},共四个.
故答案为:4.
点评 考查列举法表示集合,子集的概念,不要漏了空集∅.

练习册系列答案
相关题目
16.若$\sqrt{x}+\sqrt{y}≤a\sqrt{x+y}$(x>0,y>0)恒成立,则a的最小值为( )
| A. | 1 | B. | $\sqrt{2}$ | C. | 2 | D. | 2$\sqrt{2}$ |
20.下列各组函数中,表示同一个函数的是( )
| A. | y1=$\frac{(x+3)(x-5)}{x+3}$,y2=x-5 | B. | f(x)=x,g(x)=$\sqrt{{x}^{2}}$ | ||
| C. | f(x)=x,g(x)=$\root{3}{x^3}$ | D. | $f(x)=|x|,g(x)={({\sqrt{x}})^2}$ |
14.已知函数f(x)=$\left\{\begin{array}{l}{lo{g}_{3}x(x>0)}\\{{2}^{-x}+1(x≤0)}\end{array}\right.$,则f(f(1))+f(log2$\frac{1}{3}$)的值是( )
| A. | 6 | B. | 5 | C. | $\frac{7}{2}$ | D. | $\frac{5}{3}$ |
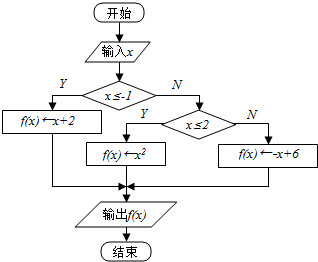 根据流程图,若函数g(x)=f(x)-m在R上有且只有两个零点,则实数m的取值范围是(-∞,0)∪(1,4).
根据流程图,若函数g(x)=f(x)-m在R上有且只有两个零点,则实数m的取值范围是(-∞,0)∪(1,4).