题目内容
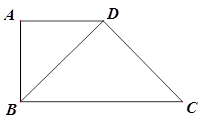
如图,梯形 中,
中,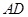
 ,
,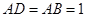 ,
,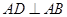 ,
,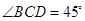 ,将
,将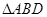 沿对角线
沿对角线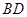 折起.设折起后点
折起.设折起后点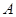 的位置为
的位置为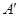 ,并且平面
,并且平面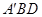
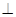 平面
平面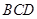 .给出下面四个命题:
.给出下面四个命题:
①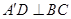 ;②三棱锥
;②三棱锥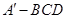 的体积为
的体积为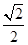 ;③
;③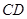
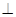 平面
平面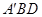 ;④平面
;④平面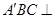 平面
平面 .
.
其中正确命题的序号是( )
| A.①② | B.③④ | C.①③ | D.②④ |
B
解析试题分析:①若 ,取
,取 的中点
的中点 ,由
,由 得,
得, ,又因为平面
,又因为平面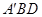
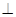 平面
平面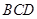 ,所以
,所以 平面
平面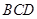 ,即
,即 ,所以
,所以 平面
平面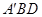 ,得
,得 ,而
,而 ,故命题不成立;②三棱锥
,故命题不成立;②三棱锥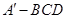 的体积为
的体积为 ,故命题不成立;③因为
,故命题不成立;③因为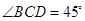 ,
,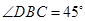 ,所以
,所以 ,又因为平面
,又因为平面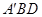
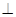 平面
平面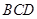 ,
, 平面
平面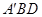 ,故命题成立;④由③知
,故命题成立;④由③知 平面
平面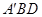 ,故
,故 ,又因为
,又因为 ,所以
,所以 平面
平面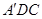 ,所以平面
,所以平面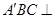 平面
平面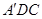 ,故命题成立;由此可得正确命题的序号是③④.
,故命题成立;由此可得正确命题的序号是③④.
考点:立体几何中垂直问题.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
设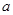 表示直线,
表示直线,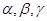 表示不同的平面,则下列命题中正确的是
表示不同的平面,则下列命题中正确的是
A.若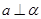 且 且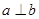 ,则 ,则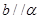 | B.若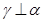 且 且 ,则 ,则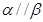 |
C.若 且 且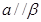 ,则 ,则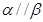 | D.若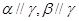 ,则 ,则 |
正四棱柱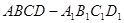 中,
中,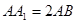 ,则异面直线
,则异面直线 所成角的余弦值为( )
所成角的余弦值为( )
A.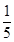 | B.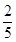 | C.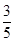 | D. |
 表示不同直线,M表示平面,给出四个命题:①若
表示不同直线,M表示平面,给出四个命题:①若 ∥M,
∥M,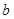 ∥M,则
∥M,则 ∥
∥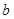 或
或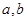 相交或
相交或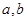 异面;②若
异面;②若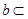 M,
M, ∥
∥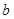 ,则
,则 ∥M;③
∥M;③ ⊥
⊥ ,
,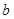 ⊥
⊥ ,则
,则 ∥
∥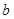 ;④
;④  ⊥M,
⊥M,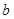 ⊥M,则
⊥M,则 ∥
∥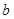 。其中正确命题为
。其中正确命题为
| A.①② | B.②③ | C.③④ | D.①④ |
设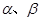 是两个不同的平面,
是两个不同的平面,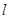 是一条直线,以下命题:
是一条直线,以下命题:
①若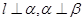 ,则
,则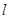 ∥
∥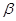 ;②若
;②若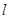 ∥
∥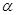 ,
,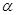 ∥
∥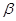 ,则
,则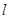 ∥
∥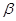 ;
;
③若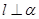 ,
,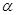 ∥
∥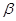 ,则
,则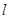
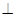
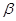 ;④若
;④若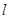 ∥
∥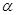 ,
,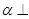
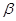 ,则
,则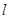
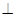
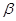 .
.
其中正确命题的个数是
| A.1个 | B.2个 | C.3个 | D.4个 |
将图(1)中的等腰直角三角形ABC沿斜边BC的中线折起得到空间四面体ABCD(如图(2)),则在空间四面体ABCD中,AD与BC的位置关系是( )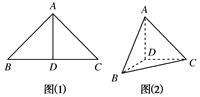
| A.相交且垂直 | B.相交但不垂直 |
| C.异面且垂直 | D.异面但不垂直 |
 中,E,F,M分别是AB、AD、
中,E,F,M分别是AB、AD、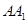 的中点,又P、Q分别在线段
的中点,又P、Q分别在线段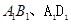 上,且
上,且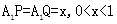 ,设面
,设面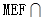 面MPQ=
面MPQ=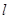 ,则下列结论中不成立的是( )
,则下列结论中不成立的是( )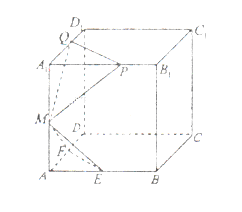
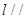 面ABCD B.
面ABCD B.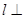 AC
AC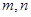 是不重合的直线,
是不重合的直线,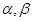 是不重合的平面,有下列命题:
是不重合的平面,有下列命题: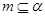 ,
,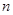 ∥
∥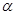 ,则
,则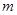 ∥
∥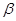 ,则
,则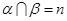 ,
,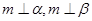 ,则
,则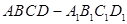 中,线段
中,线段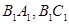 上(不包括端点)各有一点
上(不包括端点)各有一点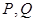 ,且
,且 ,下列说法中,不正确的是( )
,下列说法中,不正确的是( )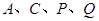 四点共面
四点共面 与平面
与平面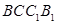 所成的角为定值
所成的角为定值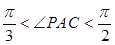
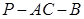 的大小为
的大小为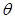 ,则
,则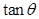 的最小值为
的最小值为