题目内容
已知棱长为l的正方体 中,E,F,M分别是AB、AD、
中,E,F,M分别是AB、AD、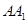 的中点,又P、Q分别在线段
的中点,又P、Q分别在线段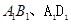 上,且
上,且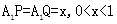 ,设面
,设面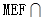 面MPQ=
面MPQ=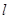 ,则下列结论中不成立的是( )
,则下列结论中不成立的是( )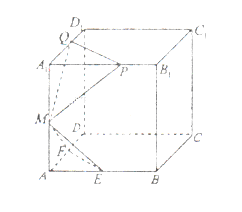
A. 面ABCD B.
面ABCD B. AC
AC
C.面MEF与面MPQ不垂直 D.当x变化时,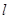 不是定直线
不是定直线
D
解析试题分析:解:连结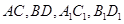 ,
,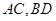 交于点
交于点
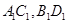 交于点
交于点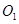
由正方体的性质知,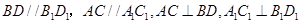
因为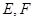 是
是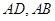 的中点,所以
的中点,所以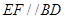
因为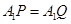 ,所以
,所以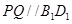
所以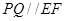 ,所以
,所以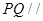 平面
平面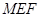 ,
,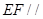 平面
平面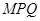 ,
,
由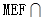 面MPQ=
面MPQ=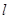 ,
,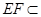 平面
平面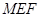 ,所以
,所以 ,而
,而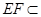 平面
平面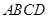 ,
,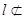 平面
平面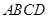 ,
,
所以,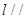 面ABCD ,所以选项A正确;
面ABCD ,所以选项A正确;
由 ,
,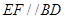 得
得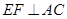 而
而 ,所以
,所以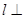 AC,所以选项B正确;
AC,所以选项B正确;
连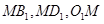 ,则
,则 而
而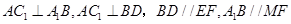
所以, ,所以
,所以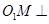 平面
平面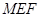 ,过直线
,过直线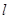 与平面
与平面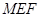 垂直的平面只能有一个,所以面MEF与面MPQ不垂直,所以选项C是正确的;
垂直的平面只能有一个,所以面MEF与面MPQ不垂直,所以选项C是正确的;
因为 ,
,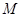 是定点,过直线外一点有且只有一条直线与已知直线平行,所以直线
是定点,过直线外一点有且只有一条直线与已知直线平行,所以直线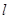 是唯一的,故选项D不正确.
是唯一的,故选项D不正确.
考点:1、直线平面的位置关系;2、直线与直线,直线与平面,平面与平面的平行与垂直的判定及性质.

练习册系列答案
相关题目
设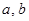 是两条不同直线,
是两条不同直线,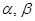 是两个不同平面,下列四个命题中正确的是( )
是两个不同平面,下列四个命题中正确的是( )
A.若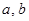 与 与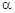 所成的角相等,则 所成的角相等,则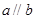 | B.若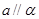 , ,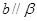 , ,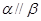 ,则 ,则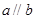 |
C.若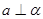 , ,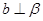 , ,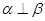 ,则 ,则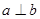 | D.若 , ,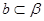 , ,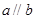 ,则 ,则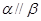 |
已知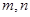 是两条不同直线,
是两条不同直线,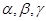 是三个不同平面,则下列正确的是 ( )
是三个不同平面,则下列正确的是 ( )
A.若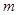 ∥ ∥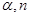 ∥ ∥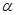 ,则 ,则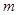 ∥ ∥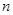 | B.若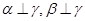 ,则 ,则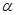 ∥ ∥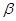 |
C.若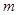 ∥ ∥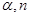 ∥ ∥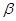 ,则 ,则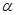 ∥ ∥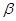 | D.若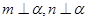 ,则 ,则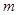 ∥ ∥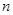 |
下列命题中,错误的是( ).
A.过平面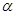 外一点可以作无数条直线与平面 外一点可以作无数条直线与平面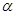 平行 平行 |
| B.与同一个平面所成的角相等的两条直线必平行 |
C.若直线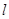 垂直平面 垂直平面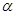 内的两条相交直线,则直线 内的两条相交直线,则直线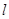 必垂直平面 必垂直平面 |
| D.垂直于同一个平面的两条直线平行 |
如图是正方体的展开图,则在这个正方体中: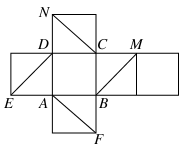
①BM与ED平行;
②CN与BE是异面直线;
③CN与BM成60°角;
④DM与BN垂直.
以上四个命题中,正确命题的序号是( )
| A.①②③ | B.②④ | C.③④ | D.②③④ |
已知m和n是两条不同的直线,α和β是两个不重合的平面,那么下面给出的条件中一定能推出m⊥β的是( )
| A.α⊥β,且m?α | B.m∥n,且n⊥β |
| C.α⊥β,且m∥α | D.m⊥n,且n∥β |
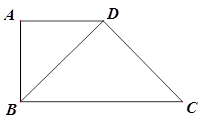
 中,
中,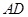
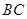 ,
,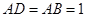 ,
,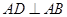 ,
,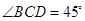 ,将
,将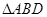 沿对角线
沿对角线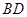 折起.设折起后点
折起.设折起后点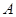 的位置为
的位置为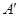 ,并且平面
,并且平面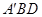
 平面
平面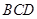 .给出下面四个命题:
.给出下面四个命题: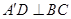 ;②三棱锥
;②三棱锥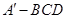 的体积为
的体积为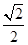 ;③
;③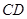
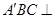 平面
平面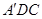 .
.