题目内容
9．等差数列{an}中，Sn表示前n项和，若a1+a3+a18+a20=20，求S20．分析 根据等差数列的性质，可得a1+a20=10，代入等差数列前n项和公式，可得答案．
解答 解：∵等差数列{an}中，a1+a3+a18+a20=20，
∴a1+a20=10，
∴S20=$\frac{1}{2}$（a1+a20）×20=100
点评 本题考查的知识点是等差数列的前n项和公式，等差数列的性质，难度不大，属于基础题．
练习册系列答案
世纪百通主体课堂小学课时同步达标系列答案
世纪百通优练测系列答案
相关题目
19．已知等差数列的首项为a1，公差为d．则该数列的通项公式为（ ）
| A． | an=a1+d（n+1） | B． | an=a1+dn | C． | an=a1+d（n-1） | D． | an=a1+d（n-2） |
17．
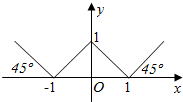函效y=f（x）的图象如图所示，则y=f（x）的解析式是（ ）
函效y=f（x）的图象如图所示，则y=f（x）的解析式是（ ）| A． | f（x）=$\left\{\begin{array}{l}{1-x，x＜1}\\{x-1，x≥1}\end{array}\right.$ | |
| B． | f（x）=$\left\{\begin{array}{l}{-x-1，x＜-1}\\{1+x，-1≤x＜0}\\{1-x，0≤x≤1}\\{x-1，x＞1}\end{array}\right.$ | |
| C． | f（x）=$\left\{\begin{array}{l}{{x}^{2}-1，x＞1或x＜-1}\\{1-{x}^{2}，-1≤x≤1}\end{array}\right.$ | |
| D． | f（x）=$\left\{\begin{array}{l}{{x}^{2}+2x+1，x≤0}\\{{x}^{2}-2x+1，x＞0}\end{array}\right.$ |
4．非零向量 $\overrightarrow{a}$，$\overrightarrow{b}$夹角为120°，且|$\overrightarrow{a}$-$\overrightarrow{b}$|=2，则|$\overrightarrow{a}$+$\overrightarrow{b}$|的取值范围为（ ）
| A． | [1，$\sqrt{3}$] | B． | [2，$\frac{4\sqrt{3}}{3}$] | C． | [$\frac{2\sqrt{3}}{3}$，4） | D． | [1，2] |