题目内容
15.已知在数列{an}中,a1=1,an+1=4n•an,求该数列的通项公式.分析 由数列递推式得到$\frac{{a}_{n+1}}{{a}_{n}}={4}^{n}$,然后利用累积法结合等差数列的前n项和得答案.
解答 解:由an+1=4n•an,得$\frac{{a}_{n+1}}{{a}_{n}}={4}^{n}$,
又a1=1,
∴当n≥2时,
${a}_{n}=\frac{{a}_{n}}{{a}_{n-1}}•\frac{{a}_{n-1}}{{a}_{n-2}}…\frac{{a}_{2}}{{a}_{1}}•{a}_{1}$
=4n-1•4n-2…41•1=4[1+2+3+…+(n-1)]=${4}^{\frac{n(n-1)}{2}}$=${2}^{{n}^{2}-n}$.
当n=1时上式成立,
∴${a}_{n}={2}^{{n}^{2}-n}$.
点评 本题考查了数列递推式,考查了累积法求数列的通项公式,是中档题.

练习册系列答案
相关题目
6.过点P(-2,2)作直线l,使直线l与两坐标轴在第二象限内围成的三角形面积为8,这样的直线l一共有( )
| A. | 3条 | B. | 2条 | C. | 1条 | D. | 0条 |
3.若圆锥的内切球与外接球的球心重合,且内切球的半径为1,则圆锥的体积为( )
| A. | π | B. | 2π | C. | 3π | D. | 4π |
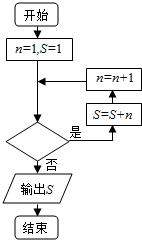 已知数列{an}中,a1=1,an+1=an+n,若利用如图所示的程序框图计算该数列的第10项的值S,则判断框内的条件是n≤9或n<10.
已知数列{an}中,a1=1,an+1=an+n,若利用如图所示的程序框图计算该数列的第10项的值S,则判断框内的条件是n≤9或n<10.