题目内容
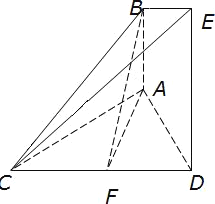
【题目】如图,已知AB⊥平面ACD,DE⊥平面ACD,△ACD为等边三角形,AD=DE=2AB,F为CD的中点.
(1)求证:AF∥平面BCE;
(2)求证:平面BCE⊥平面CDE;
(3)求直线BF和平面BCE所成角的正弦值.
【答案】(1)见解析(2)见解析(3)![]()
【解析】
(1)取CE的中点G,由三角形的中位线性质证明四边形GFAB为平行四边形,得到AF∥BG,从而证明AF∥平面BCE.
(2)通过证明AF⊥CD,DE⊥AF,从而证明AF⊥平面CDE,再利用BG∥AF证明BG⊥平面CDE,进而证明平面BCE⊥平面CDE.
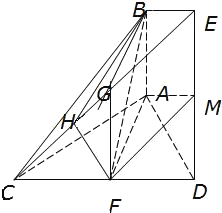
(3)在平面CDE内,过F作FH⊥CE于H,由平面BCE⊥平面CDE,得 FH⊥平面BCE,故∠FBH为BF和平面BCE所成的角,解Rt△FHB求出∠FBH的正弦值.
(1)证明:取CE的中点G,连FG、BG.
∵F为CD的中点,∴GF∥DE且![]() .
.
∵AB⊥平面ACD,DE⊥平面ACD,
∴AB∥DE,∴GF∥AB.
又![]() ,∴GF=AB.
,∴GF=AB.
∴四边形GFAB为平行四边形,则AF∥BG.
∵AF平面BCE,BG平面BCE,
∴AF∥平面BCE.
(2)证明:∵△ACD为等边三角形,F为CD的中点,∴AF⊥CD.
∵DE⊥平面ACD,AF平面ACD,∴DE⊥AF.
又CD∩DE=D,故AF⊥平面CDE.
∵BG∥AF,∴BG⊥平面CDE.
∵BG平面BCE,
∴平面BCE⊥平面CDE.
(3)解:在平面CDE内,过F作FH⊥CE于H,连BH.
∵平面BCE⊥平面CDE,∴FH⊥平面BCE.
∴∠FBH为BF和平面BCE所成的角.
设AD=DE=2AB=2a,则![]() ,
,![]() ,
,
Rt△FHB中,![]() .
.
∴直线BF和平面BCE所成角的正弦值为![]() .
.

练习册系列答案
相关题目