题目内容
19.如图,直线y=kx分抛物线y=x-x2与x轴所围图形为上下两部分面积比为1:7,则k的值为( )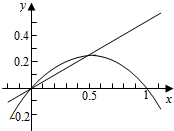
| A. | 1 | B. | $\sqrt{2}$-1 | C. | 0.5 | D. | 0.4 |
分析 确定交点的坐标,根据上下部分的面积比为1:7得到∫01-k[(x-x2)-kx]dx=$\frac{1}{8}$∫01(x-x2)dx,利用定积分的计算公式即可求得k值.
解答 解:由kx=x-x2,可得x=0或x=1-k(0<k<1).
∵直线y=kx分抛物线y=x-x2与x轴所围图形为上下两部分面积比为1:7,
∴由题设得∫${\;}_{0}^{1-k}$[(x-x2)-kx]dx=$\frac{1}{8}$∫${\;}_{0}^{1}$(x-x2)dx
即∫${\;}_{0}^{1-k}$[(x-x2)-kx]dx=$\frac{1}{8}$($\frac{1}{2}$x2-$\frac{1}{3}$x3 )|${\;}_{0}^{1}$=$\frac{1}{48}$
∴$\frac{1}{6}$(1-k)3=$\frac{1}{48}$,
∴(1-k)3=$\frac{1}{8}$,
即1-k=$\frac{1}{2}$,
∴k=$\frac{1}{2}$=0.5.
故选:C.
点评 本题主要考查利用积分求区域面积,求出交点坐标结合积分公式是解决本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目