题目内容
9.已知 $\vec a$=(2,3),$\vec b$=(-3,4),则$\vec a$在$\vec b$方向上的投影为$\frac{6}{5}$.分析 根据投影的定义,应用公式|$\overrightarrow{a}$|cos<$\overrightarrow{a}$,$\overrightarrow{b}$>=$\frac{\overrightarrow{a}\overrightarrow{b}}{|\overrightarrow{b}|}$,结合坐标求解即可.
解答 解:∵$\vec a$=(2,3),$\vec b$=(-3,4),
∴$\overrightarrow{a}$$•\overrightarrow{b}$=-6+12=6,
根据投影的定义可得:
$\vec a$在$\vec b$方向上的投影为|$\overrightarrow{a}$|cos<$\overrightarrow{a}$,$\overrightarrow{b}$>=$\frac{\overrightarrow{a}\overrightarrow{b}}{|\overrightarrow{b}|}$=$\frac{6}{\sqrt{9+16}}$=$\frac{6}{5}$,
故答案为:$\frac{6}{5}$.
点评 本题主要考查向量投影的定义及求解的方法,公式与定义两者要灵活运用.解答关键在于要求熟练应用公式

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案
相关题目
17.某单位为了了解用电量y度与气温x℃之间的关系,随机统计了某4天的用电量与当天气温,并制作了对照表:由表中数据得线性回归方程$\widehat{y}$=bx+a中b=-2,预测当气温为-4℃时,用电量的度数约为( )
| 气温(℃) | 18 | 13 | 10 | -1 |
| 用电量(度) | 24 | 34 | 38 | 64 |
| A. | 70 | B. | 69 | C. | 68 | D. | 67 |
4.已知f(x)、g(x)均为[-1,3]上连续不断的曲线,根据下表能判断方程f(x)=g(x)有实数解的区间是( )
| x | -1 | 0 | 1 | 2 | 3 |
| f(x) | -0.677 | 3.011 | 5.432 | 5.980 | 7.651 |
| g(x) | -0.530 | 3.451 | 4.890 | 5.241 | 6.892 |
| A. | (-1,0) | B. | (1,2) | C. | (0,1) | D. | (2,3) |
14.观察数列1,2,2,3,3,3,4,4,4,4,…的特点,问第100项为( )
| A. | 10 | B. | 14 | C. | 13 | D. | 100 |
1.设单位向量$\overrightarrow{a}$,$\overrightarrow{b}$满足|$\overrightarrow{a}$+$\overrightarrow{b}$|=1,则sin$<\overrightarrow{a},\overrightarrow{b}>$等于( )
| A. | $\frac{3}{5}$ | B. | $\frac{1}{3}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
19.如图,直线y=kx分抛物线y=x-x2与x轴所围图形为上下两部分面积比为1:7,则k的值为( )
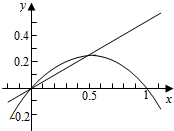

| A. | 1 | B. | $\sqrt{2}$-1 | C. | 0.5 | D. | 0.4 |