题目内容

10．若函数f（x）=x3-ax2-2ax+a2-1在其定义域内不存在递减区间，则实数a的取值范围是[-6，0]．

分析 先求出函数的导数，结合二次函数的性质，得到不等式，解出即可．

解答 解：∵f′（x）=3x2-2ax-2a，
若函数f（x）在其定义域内不存在递减区间，
∴f′（x）的图象不在x轴下方，
∴△=4a2+24a≤0，解得：-6≤x≤0，
故答案为：[-6，0]．

点评 本题考查了函数的单调性，考查导数的应用，是一道基础题．

练习册系列答案
相关题目
20．数列{an}中，a1=2，a2=7，an+2是anan+1的个位数字，Sn是{an}的前n项和，则S242-10a6=909．
1．设单位向量$\overrightarrow{a}$，$\overrightarrow{b}$满足|$\overrightarrow{a}$+$\overrightarrow{b}$|=1，则sin$＜\overrightarrow{a}，\overrightarrow{b}＞$等于（　　）
A．$\frac{3}{5}$B．$\frac{1}{3}$C．$\frac{\sqrt{2}}{2}$D．$\frac{\sqrt{3}}{2}$
18．已知函数$y=Asin（ωx+φ）+B（A＞0，ω＞0，|φ|＜\frac{π}{2}）$在同一个周期上的最高点为（2，2），最低点为（8，-4）．
（1）求函数解析式．
（2）求出f（x）的单调递增区间；
（3）指出当f（x）取得最大值和最小值时x的集合．
5．已知函数f（x）=x2-a|x-1|，a＞0
（1）当a=1时，求函数f（x）的单调区间；
（2）若区间[1，4]内f（x）＞0恒成立，求a的取值范围；
（3）记函数f（x）在区间[0，3]内的最大值，最小值分别为M（a），m（a），求M（a）-m（a）
15．已知函数f（x）=loga（1+x）-loga（1-x）（a＞0，a≠1）．
（Ⅰ）判断f（x）奇偶性，并证明；
（Ⅱ）当0＜a＜1时，解不等式f（x）＞0．
2．函数y=f（x）的图象在点x=5处的切线方程是y=-x+8，则f（5）+f′（5）=（　　）
A．0B．1C．2D．3
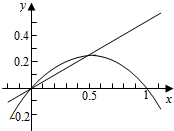
19．如图，直线y=kx分抛物线y=x-x2与x轴所围图形为上下两部分面积比为1：7，则k的值为（　　）
A．1B．$\sqrt{2}$-1C．0.5D．0.4
20．数列{an}的前n项和为Sn，且满足Sn=2an+1，则a5=-16．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网