题目内容
【题目】以平面直角坐标系![]() 的原点为极点,
的原点为极点, ![]() 轴正半轴为极轴且取相同的单位长度建立极坐标系.已知点
轴正半轴为极轴且取相同的单位长度建立极坐标系.已知点![]() 的参数方程为
的参数方程为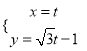 (
(![]() 为参数),点
为参数),点![]() 在曲线
在曲线![]() 上.
上.
(1)求在平面直角坐标系![]() 中点
中点![]() 的轨迹方程和曲线
的轨迹方程和曲线![]() 的普通方程;
的普通方程;
(2)求![]() 的最大值.
的最大值.
【答案】(1)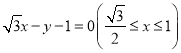 ,曲线
,曲线![]() 的普通方程为
的普通方程为![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)消参的普通方程,利用转化公式极坐标化普通方程;(2)数形结合,转化为线段上一点与圆上一点距离的最大值,注意利用垂线段最短及点与圆上点距离最大值的求法.
试题解析:(1)由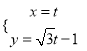 消去参数
消去参数![]() ,得
,得![]() ,
,
又![]() ,∴
,∴![]() ,
,
故点![]() 的轨迹方程是
的轨迹方程是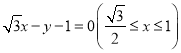 ,
,
∵![]() ,∴
,∴![]() ,∴
,∴![]() ,即
,即![]() ,
,
故曲线![]() 的普通方程为
的普通方程为![]() .
.
(2)如图:
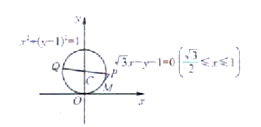
由题意可得,点![]() 的线段
的线段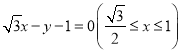 上,点
上,点![]() 在圆
在圆![]() 上,
上,
∵圆![]() 的圆心
的圆心![]() 到直线
到直线![]() 的距离
的距离![]() ,
,
∴直线![]() 与圆
与圆![]() 相切,且切点为
相切,且切点为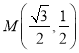 ,
,
易知线段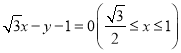 上存在一点
上存在一点![]() ,
,
则点![]() 与圆心
与圆心![]() 的连线
的连线![]() ,与圆的交点
,与圆的交点![]() 满足
满足![]() 取最大值.
取最大值.
即当点![]() 坐标为
坐标为![]() 时,
时, ![]() 取最大值.
取最大值.
∵![]() ,
,
∴![]() 的最大值为
的最大值为![]() .
.

练习册系列答案
相关题目
【题目】某品牌连锁便利店有![]() 个分店,A,B,C三种商品在各分店均有销售,这三种商品的单价和重量如表1所示:
个分店,A,B,C三种商品在各分店均有销售,这三种商品的单价和重量如表1所示:
商品A | 商品B | 商品C | |
单价(元) | 15 | 20 | 30 |
每件重量(千克) | 0.2 | 0.3 | 0.4 |
表1
某日总店向各分店分配的商品A,B,C的数量如表2所示:
商品 分店 | 分店1 | 分店2 | …… | 分店 |
A | 12 | 20 | m1 | |
B | 15 | 20 | m2 | |
C | 20 | 15 | m3 |
表2
表3表示该日分配到各分店去的商品A,B,C的总价和总重量:
分店1 | 分店2 | …… | 分店 | |
总价(元) |
| |||
总重量(千克) |
|
表3
则![]() __________ ;
__________ ; ![]() __________ .
__________ .