题目内容
已知函数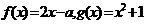 ,
,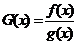 ,
,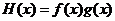 .
.
(Ⅰ)当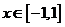 ,求使
,求使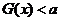 恒成立的
恒成立的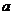 的取值范围;
的取值范围;
(Ⅱ)设方程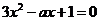 的两根为
的两根为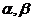 (
(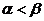 ),且函数
),且函数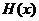 在区间
在区间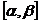 上的最大值与最小值之差是8,求
上的最大值与最小值之差是8,求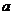 的值.
的值.
【答案】
解:(Ⅰ)由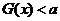 得
得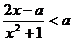 ,即
,即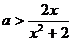 .下求
.下求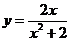 在
在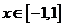 上的最大值,当
上的最大值,当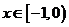 时,
时,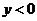 ;当
;当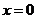 时
时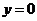 ;当
;当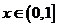 时,
时,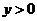 ,
, 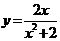 =
=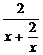 可证其在
可证其在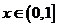 上是增函数,故在
上是增函数,故在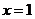 时取最大值
时取最大值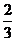 .∴
.∴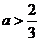 .7分
.7分
(Ⅱ)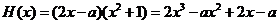 ,
, .
.
由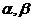 是方程
是方程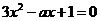 的两根,可知
的两根,可知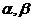 是方程
是方程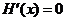 的两根.
的两根.
故当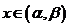 时,
时, 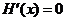 ,从而
,从而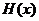 在
在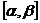 上是减函数,
上是减函数,
又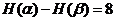 ,
,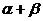 =
=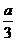 ,
,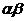 =
=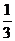 ,
,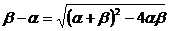 =
=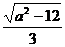 ,
,
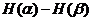 =|
=|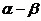 |
|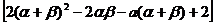
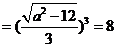 ,
,
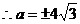 .
….…15分
.
….…15分

练习册系列答案
相关题目
 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<| π |
| 2 |
A、f(x)=2sin(
| ||||
B、f(x)=2sin(
| ||||
C、f(x)=2sin(2x-
| ||||
D、f(x)=2sin(2x+
|