题目内容
已知复平面内点A、B对应的复数分别是z1＝sin2
＋i，z2＝－cos2＋icos2，其中∈(0，2π)，设
对应的复数为z．
(1)求复数z；
(2)若复数z对应的点P在直线y＝
上，求的值．
答案：
解析：
解析：
|
解：(1)z＝z2－z1＝－cos2 ＝－1－2sin2 (2)点P的坐标为(－1，－2sin2 由点P在直线y＝ 所以sin2 因为 点评：注意 |
－sin2
上，得－2sin2
．
，则sin
．
，
，
，
．
练习册系列答案
学练快车道口算心算速算天天练系列答案
相关题目
已知复平面内点A，B对应的复数分别是z1＝sin2θ＋i，z2＝－cos2θ＋icos2θ，其中θ∈(0，2π)，设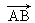
对应的复数为z．
(Ⅰ)求复数z；
(Ⅱ)若复数z对应的点P在直线y＝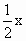
上，求θ的值．
已知复平面内点A，B对应的复数分别是z1＝sin2θ＋i，z2＝－cos2θ＋icos2θ，其中θ∈(0，2π)，设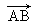
对应的复数为z．
(Ⅰ)求复数z；
(Ⅱ)若复数z对应的点P在直线y＝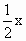
上，求θ的值．
＋i，z2＝－cos2
对应的复数为z．
x上，求
对应的复数为z. 
x上，求θ的值. 
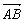对应的复数为z.
x上，求θ的值.