题目内容
已知复平面内点A、B对应的复数分别是z1=sin2θ+i,z2=-cos2θ+icos2θ，其中θ∈（0，2π），设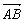
对应的复数为z. （1）求复数z；
（2）若复数z对应的点P在直线y=
x上，求θ的值.
解：（1）z=z2-z1=-cos2θ-sin2θ+i(cos2θ-1)=-1-2sin2θ·i.?
（2）点P的坐标为（-1，-2sin2θ）,?
由点P在直线y=
x上，得-2sin2θ=-.?
所以sin2θ=
，则sinθ=±
.?
因为θ∈(0,2π),所以θ=
，
，
，
.
点评：注意θ的范围限制，本题是与三角函数相结合的小综合题目，这就要求对三角函数的相应知识要掌握清楚.
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
已知复平面内点A，B对应的复数分别是z1＝sin2θ＋i，z2＝－cos2θ＋icos2θ，其中θ∈(0，2π)，设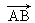
对应的复数为z．
(Ⅰ)求复数z；
(Ⅱ)若复数z对应的点P在直线y＝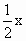
上，求θ的值．
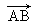对应的复数为z．
上，求θ的值．
＋i，z2＝－cos2
对应的复数为z．
x上，求
对应的复数为z.
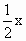x上，求θ的值.