题目内容
已知复平面内点A,B对应的复数分别是z1=sin2θ+i,z2=-cos2θ+icos2θ,其中θ∈(0,2π),设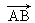 对应的复数为z.
对应的复数为z.
(Ⅰ)求复数z;
(Ⅱ)若复数z对应的点P在直线y=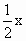 上,求θ的值.
上,求θ的值.
答案:
解析:
解析:
|
(Ⅰ)解:z=z2-z1=-cos2θ-sin2θ+i(cos2θ-1) =-1-2isin2θ (Ⅱ)解:点P的坐标为(-1,-2sin2θ) 由点P在直线y= ∴sin2θ= ∵θ∈(0,2π) ∴θ= |

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
已知复平面内点A,B对应的复数分别是z1=sin2θ+i,z2=-cos2θ+icos2θ,其中θ∈(0,2π),设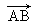 对应的复数为z.
对应的复数为z.
(Ⅰ)求复数z;
(Ⅱ)若复数z对应的点P在直线y=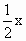 上,求θ的值.
上,求θ的值.
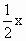 上,得-2sin2θ=
上,得-2sin2θ=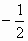 .
.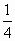 则sinθ=
则sinθ=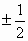 .
.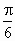 ,
,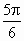 ,
,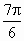 ,
,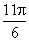 .
.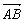 对应的复数为z.
对应的复数为z.