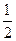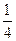题目内容
（文科）某工厂要建造一个长方体的无盖贮水池，其容积为4800m3，深为3m，如果池底造价为每平方米150元，池壁每平方米造价为120元，怎么设计水池能使总造价最低？最低造价是多少？
设底面的长为xm，宽为ym，水池总造价为z元，根据题意，有
z=150×
+120（2×3x+2×3y）=240000+720（x+y）
由容积为4800m3，可得
3xy=4800，
即xy=1600；
由基本不等式与不等式的性质，可得
240000+720（x+y）≥240000+720×2
，
即z≥240000+720×2
，
∴z≥297600；
当x=y，即x=y=40时，“=”成立；
所以，将水池的底面设计成边长为40m的正方形时总造价最低，最低总造价是297600元．
z=150×
| 4800 |
| 3 |
由容积为4800m3，可得
3xy=4800，
即xy=1600；
由基本不等式与不等式的性质，可得
240000+720（x+y）≥240000+720×2
| xy |
即z≥240000+720×2
| 1600 |
∴z≥297600；
当x=y，即x=y=40时，“=”成立；
所以，将水池的底面设计成边长为40m的正方形时总造价最低，最低总造价是297600元．
练习册系列答案
相关题目
