题目内容
5.锐角△ABC的内角A,B,C的对边分别为a,b,c,A=60°a=3,则△ABC的周长的取值范围( )| A. | [6,9] | B. | [3$\sqrt{3}$+3,9) | C. | (6,9] | D. | (3$\sqrt{3}$+3,9] |
分析 由正弦定理可得:$\frac{b}{sinB}$=$\frac{c}{sinC}$=$\frac{a}{sinA}$=$\frac{3}{sin60°}$=2$\sqrt{3}$,b=2$\sqrt{3}$sinB,c=2$\sqrt{3}$sinC,于是a+b+c=3+2$\sqrt{3}$sinB+2$\sqrt{3}$sin( $\frac{2π}{3}$-B)化简整理即可得出.
解答 解:由正弦定理可得:$\frac{b}{sinB}$=$\frac{c}{sinC}$=$\frac{a}{sinA}$=$\frac{3}{sin60°}$=2$\sqrt{3}$,
∴b=2$\sqrt{3}$sinB,c=2$\sqrt{3}$sinC,
∴a+b+c=3+2$\sqrt{3}$sinB+2$\sqrt{3}$sinC=3+2$\sqrt{3}$sinB+2$\sqrt{3}$sin($\frac{2π}{3}$-B)=3+3$\sqrt{3}$sinB+3cosB=6sin(B+$\frac{π}{6}$)+3,
∵$\frac{π}{6}$<B<$\frac{π}{2}$,
∴$\frac{π}{3}$<B+$\frac{π}{6}$<$\frac{2π}{3}$,
∴sin(B+$\frac{π}{6}$)∈($\frac{\sqrt{3}}{2}$,1],
∴(a+b+c)∈(3+3$\sqrt{3}$,9].
故选:D.
点评 本题主要考查正弦定理、诱导公式、两角和与差的余弦公式等基础知识,考查了考生运算求解的能力,属于中档题.

练习册系列答案
相关题目
14.复数z=$\frac{(1+i)^{2}}{1-i}$的共轭复数所对应的点位于复平面的( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
13.已知$\overrightarrow a=(1,2)$,$\overrightarrow b=(2x,-3)$且$\overrightarrow a∥\overrightarrow b$,则x=( )
| A. | -3 | B. | -$\frac{3}{4}$ | C. | 0 | D. | $\frac{3}{4}$ |
10.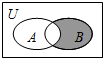 设全集U是实数集R,集合A={y|y=3x,x>0},B={x|y=$\sqrt{2x-{x}^{2}}$},则图中阴影部分所表示的集合是( )
设全集U是实数集R,集合A={y|y=3x,x>0},B={x|y=$\sqrt{2x-{x}^{2}}$},则图中阴影部分所表示的集合是( )
 设全集U是实数集R,集合A={y|y=3x,x>0},B={x|y=$\sqrt{2x-{x}^{2}}$},则图中阴影部分所表示的集合是( )
设全集U是实数集R,集合A={y|y=3x,x>0},B={x|y=$\sqrt{2x-{x}^{2}}$},则图中阴影部分所表示的集合是( )| A. | {x|0≤x<1} | B. | {x|0≤x≤1} | C. | {x|1<x<2} | D. | {x|1<x≤2} |
17.若直线l的斜率$k=-\frac{{\sqrt{3}}}{3}$,则其倾斜角为( )
| A. | 30° | B. | 60° | C. | 120° | D. | 150° |