题目内容
【题目】已知函数f(x)=x2+|x|﹣|x﹣5|+2.
(1)求不等式f(x)<0的解集;
(2)若关于x的不等式|f(x)|≤m的整数解仅有11个,求m的取值范围.
【答案】
(1)解:当x≤0时,f(x)=x2﹣x+x﹣5+2=x2﹣3,
由x2﹣3<0解得﹣ ![]() <x<
<x< ![]() ,取﹣
,取﹣ ![]() <x≤0;
<x≤0;
当0<x<5时,f(x)=x2+x+x﹣5+2=x2+2x﹣3,
由x2+2x﹣3<0解得﹣3<x<1,取0<x<1;
当x≥5时,f(x)=x2+x﹣x+5+2=x2+7,
由x2+7<0无解;
综上,不等式f(x)<0的解集为(﹣ ![]() ,1)
,1)
(2)解:由(1)知,f(x)=  ,
,
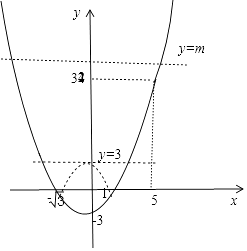
画出f(x)的图象如图所示;
若关于x的不等式|f(x)|≤m的整数解仅有11个,
当m=32时,由x2+7≤32,解得x≤5;
由x2﹣3≤32,解得﹣ ![]() ≤x,
≤x,
满足不等式|f(x)|≤m的整数解仅有11个;
当m=33时,由x2+7≤33,解得x≤ ![]() ;
;
由x2﹣3≤33,解得﹣6≤x,
满足不等式|f(x)|≤m的整数解仅有12个;
不满足题意;
当m=31时,由x2+7≤31,解得x≤ ![]() ;
;
由x2﹣3≤31,解得﹣ ![]() ≤x,
≤x,
满足不等式|f(x)|≤m的整数解仅有10个;
不满足题意;
综上,m的取值范围是[32,33).
【解析】(1)讨论x的取值,去掉绝对值,化简f(x),求出不等式f(x)<0的解集;(2)由(1)写出f(x)解析式,画出f(x)的图象,结合图象,求出不等式|f(x)|≤m的整数解仅有11个时,求出m的取值范围.
【考点精析】关于本题考查的绝对值不等式的解法,需要了解含绝对值不等式的解法:定义法、平方法、同解变形法,其同解定理有;规律:关键是去掉绝对值的符号才能得出正确答案.

练习册系列答案
相关题目