题目内容
数列{an}满足a1+2a2+22a3+…+2n-1an=4n.
(1)求通项an;
(2)求数列{an}的前n项和 Sn.
(1)求通项an;
(2)求数列{an}的前n项和 Sn.
(1)an=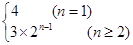
(2)Sn=3×2 n-2
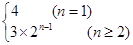
(2)Sn=3×2 n-2
(1)a1+2a2+22a3+…+2n-1an=4n,
∴a1+2a2+22a3+…+2nan+1=4n+1,相减得2n an+1=3×4n, ∴an+1=3×2n,
又n=1时a1=4,∴综上an=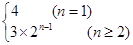 为所求;
为所求;
(2)n≥2时,Sn=4+3(2n-2), 又n=1时S1=4也成立,
∴Sn=3×2 n-2
∴a1+2a2+22a3+…+2nan+1=4n+1,相减得2n an+1=3×4n, ∴an+1=3×2n,
又n=1时a1=4,∴综上an=
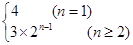 为所求;
为所求;(2)n≥2时,Sn=4+3(2n-2), 又n=1时S1=4也成立,
∴Sn=3×2 n-2

练习册系列答案
相关题目
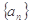 的前
的前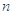 项和为
项和为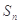 ,对一切
,对一切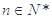 ,点
,点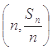 都在函数
都在函数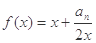 的图象上
的图象上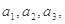 归纳数列
归纳数列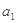 ),
),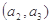 ,
,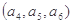 ,
,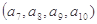 ;
;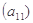 ,
,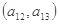 ,
,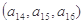 ,
,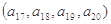 ;
;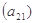 ,…..,
,…..,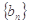 ,
,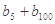 的值;
的值;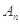 为数列
为数列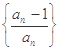 的前
的前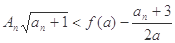 对一切
对一切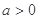 ,求
,求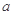 的取值范围
的取值范围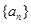 中,
中,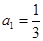 ,且前n项的算术平均数等于第n项的
,且前n项的算术平均数等于第n项的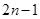 倍(
倍(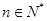 ).
). 满足:
满足: (m为正整数),
(m为正整数), 若
若 ,则m所有可能的取值为________。
,则m所有可能的取值为________。 中,
中, ,则
,则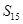 = .
= .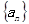 的前
的前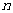 项和为
项和为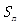 ,且
,且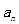 是
是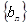 满足
满足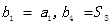 .
.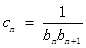 ,数列
,数列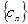 的前n项和为
的前n项和为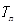 ,若
,若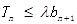 对一切
对一切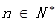 恒成立,求实数
恒成立,求实数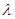 的最小值.
的最小值.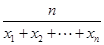 为n个正数x1,x2,…,xn的“平均倒数”,若正项数列{cn}的前n项的“平均倒数”为
为n个正数x1,x2,…,xn的“平均倒数”,若正项数列{cn}的前n项的“平均倒数”为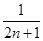 ,则数列{cn}的通项公式为cn=________.
,则数列{cn}的通项公式为cn=________.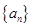 中,
中, ,那么数列
,那么数列