Question

【题目】已知f（x）= ，且g（x）=f（x）+ 有三个零点，则实数a的取值范围为 ．

Answer 1

【答案】（,∞）
【解析】解：函数g（x）=f（x）+ 有三个零点，即方程f（x）+ =0有三个根，

也就是函数y=f（x）的图象与y=﹣ 的图象有三个不同交点．

如图：

y=﹣ 与y=ln（1﹣x）（x＜0）一定有一交点；

当a≤0时，y=x2﹣ax（x≥0）的图象是图中虚线部分，

∴函数y=f（x）的图象与y=﹣ 的图象有两个不同交点，不满足题意；

当a＞0时，联立 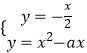，得2x2﹣（2a﹣1）x=0．

若函数y=f（x）的图象与y=﹣ 的图象有三个不同交点，则方程2x2﹣（2a﹣1）x=0有一0根一正根，

则 ，即a＞ ．

∴实数a的取值范围为：（ ，+∞）．

所以答案是：（ ，+∞）．