题目内容
12.在等比数列{an}中,a1=1,且a2是a1与a3-1的等差中项.(1)求数列{an}的通项公式;
(2)若数列{bn}满足${b_n}=\frac{{1+n(n+1){a_n}}}{n(n+1)}(n∈{N^*})$.求数列{bn}的前n项和$S_n^{\;}$.
分析 (1)设等比数列{an}的公比为q,运用等差数列的性质和等比数列的通项公式,解方程可得公比q,即可得到所求通项公式;
(2)化简bn=2n-1+($\frac{1}{n}$-$\frac{1}{n+1}$),运用分组求和和裂项相消求和,化简即可得到所求和.
解答 解:(1)设等比数列{an}的公比为q,
a2是a1与a3-1的等差中项,即有a1+a3-1=2a2,
即为1+q2-1=2q,解得q=2,
即有an=a1qn-1=2n-1;
(2)${b_n}=\frac{{1+n(n+1){a_n}}}{n(n+1)}(n∈{N^*})$=an+$\frac{1}{n(n+1)}$
=2n-1+($\frac{1}{n}$-$\frac{1}{n+1}$),
数列{bn}的前n项和$S_n^{\;}$=(1+2+22+…+2n-1)+(1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{4}$+…+$\frac{1}{n}$-$\frac{1}{n+1}$)
=$\frac{1-{2}^{n}}{1-2}$+1-$\frac{1}{n+1}$=2n-$\frac{1}{n+1}$.
点评 本题考查等差数列和等比数列的通项和求和公式的运用,考查数列的求和方法:分组求和和裂项相消求和,考查运算能力,属于中档题.

练习册系列答案
相关题目
20.已知幂函数y=(a2-2a-2)xa在实数集R上单调,那么实数a=( )
| A. | 一切实数 | B. | 3或-1 | C. | -1 | D. | 3 |
7.若非零向量$\vec a$与向量$\vec b$的夹角为钝角,$|{\vec b}|=2$,且当t=-2时,$|{\vec b-t\vec a}|$(t∈R)取最小值$\frac{6}{5}$,则$\vec a•({\vec b-\vec a})$等于( )
| A. | $-\frac{48}{25}$ | B. | -2 | C. | $-\frac{11}{5}$ | D. | $\frac{9}{5}$ |
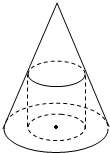 已知:如图所示,一个圆锥的底面半径为30,高为40,在其中有一个高为20的内接圆柱.
已知:如图所示,一个圆锥的底面半径为30,高为40,在其中有一个高为20的内接圆柱.